Question

（08年汕头市二模理）（14分） 在平面区域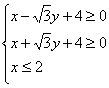内作圆，其中面积最大的圆记为⊙．

（Ⅰ）试求出⊙的方程；

（Ⅱ）圆与轴相交于、两点，圆内的动点使、、成等比数列，求的取值范围．

Answer 1

解析 ：（Ⅰ）解法一：由概率知识得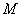；⊙为三角形区域的内切圆。              2分

设⊙的方程为，则点在所给区域的内部．

于是有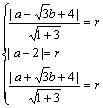                 4分

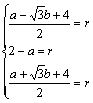  即                     6分

解得:,所求圆方程为：。                         7分

解法二：由已知条件知，⊙为三角形区域的内切圆。

设由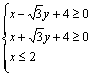确定的区域为（如图）。

直线与直线关于轴对称，且的倾斜角为，

\三角形的一个内角为 。                 2分

直线与的平分线垂直，点，，\为正三角形， 5分

且三角形的高为6，内切圆圆心为的重心，即，半径为，

\所求圆方程为：。                                            7分

（Ⅱ）不妨设，,。由即得，。        8分

设，由、、成等比数列，

得， 即．                   10分

              12分

由于点在圆内，故

由此得．所以的取值范围为．                       14分