题目内容
已知等差数列的首项a1和公差d是方程x2-2x-3=0的两根,且知d>a1,则这个数列的第30项是
- A.86
- B.85
- C.84
- D.83
A
分析:由等差数列的首项a1和公差d是方程x2-2x-3=0的两根,d>a1,解方程x2-2x-3=0,得a1=-1,d=3,由此利用等差数列的通项公式能够求出这个数列的第30项.
解答:等差数列的首项a1和公差d是方程x2-2x-3=0的两根,d>a1,
解方程x2-2x-3=0,得x1=-1,x2=3,
∴a1=-1,d=3,
∴a30=-1+29×3=86.
故选A.
点评:本题考查等差数列的通项公式的求法,是基础题.解题时要认真审题,仔细解答.
分析:由等差数列的首项a1和公差d是方程x2-2x-3=0的两根,d>a1,解方程x2-2x-3=0,得a1=-1,d=3,由此利用等差数列的通项公式能够求出这个数列的第30项.
解答:等差数列的首项a1和公差d是方程x2-2x-3=0的两根,d>a1,
解方程x2-2x-3=0,得x1=-1,x2=3,
∴a1=-1,d=3,
∴a30=-1+29×3=86.
故选A.
点评:本题考查等差数列的通项公式的求法,是基础题.解题时要认真审题,仔细解答.

练习册系列答案
相关题目
 的首项为a,公差为b,等比数列
的首项为a,公差为b,等比数列 的首项为b,公比为a,其中a、b都是大于1的正整数,且
的首项为b,公比为a,其中a、b都是大于1的正整数,且 。
。 ,总存在
,总存在 ,使得
,使得 成立,求b;
成立,求b; ,问数列
,问数列 中是否存在连续三项成等比数列,若存在,求出所有成等比数列的连续三项,若不存在,请说明理由。(14分)
中是否存在连续三项成等比数列,若存在,求出所有成等比数列的连续三项,若不存在,请说明理由。(14分)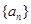 的首项为a,公差为b,等比数列
的首项为a,公差为b,等比数列 的首项为b,公比为a,其中a,b均为正整数,若
的首项为b,公比为a,其中a,b均为正整数,若 。
。 成等比数列,求数列
成等比数列,求数列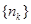 的通项公式。
的通项公式。
 的前n项和为
的前n项和为 ,求当
,求当 最大时,n的值。
最大时,n的值。 的首项为
的首项为 ,公差为b,等比数列
,公差为b,等比数列 的首项为b,公比为a(其中a,b均为正整数)。
的首项为b,公比为a(其中a,b均为正整数)。 ,求数列
,求数列 的通项公式;
的通项公式; ,对任意
,对任意 在
在 之间插入
之间插入 个2,得到一个新的数列
个2,得到一个新的数列 ,试求满足等式
,试求满足等式 的所有正整数m的值;
的所有正整数m的值; ,若存在正整数m,n以及至少三个不同的b值使得等
,若存在正整数m,n以及至少三个不同的b值使得等 成立,求t的最小值,并求t最小时a,b的值。
成立,求t的最小值,并求t最小时a,b的值。 的首项为a,公差为b;等比数列
的首项为a,公差为b;等比数列 的首项为b,公比为a,其中a,
的首项为b,公比为a,其中a, ,且
,且 .
. ,总存在
,总存在 ,使
,使 ,求b的值;
,求b的值; 是所有
是所有 为
为 是
是 .
.