题目内容
已知等差数列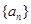 的首项为a,公差为b,等比数列
的首项为a,公差为b,等比数列 的首项为b,公比为a,其中a,b均为正整数,若
的首项为b,公比为a,其中a,b均为正整数,若 。
。
(1)求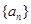 、
、 的通项公式;
的通项公式;
(2)若 成等比数列,求数列
成等比数列,求数列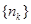 的通项公式。
的通项公式。
(3)设
 的前n项和为
的前n项和为 ,求当
,求当 最大时,n的值。
最大时,n的值。
【答案】
(1)
(2)
(3)
【解析】(1)根据 ,可得到关于a,b的两个方程,再a,b均为正整数,可解得a,b的值,进而通项可求。
,可得到关于a,b的两个方程,再a,b均为正整数,可解得a,b的值,进而通项可求。
(2)在第(1)问的基础上可得 以2为首项,3为公比的等比数列,所以
以2为首项,3为公比的等比数列,所以 ,再根据
,再根据 ,就可得
,就可得 .
.
(3)先求出 ,进而求出
,进而求出 ,所以可知
,所以可知 是一个等差数列,所以求出
是一个等差数列,所以求出 的前n项和,再根据二次函数求最值的方法即可得解。
的前n项和,再根据二次函数求最值的方法即可得解。
解:(1)由题得 ,
,
(2)由(1)得:
∴ 以2为首项,3为公比的等比数列 ∴
以2为首项,3为公比的等比数列 ∴ ,
,
又由(1)得: ∴
∴
(3)

 (10分)
(10分)

 ≤8时,
≤8时, >0。
>0。

 当
当 >9时,
>9时, <0
(13分)
<0
(13分)


练习册系列答案
相关题目
 的首项为
的首项为 ,公差为
,公差为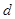 ,其前
,其前 项和为
项和为 ,若直线
,若直线 与圆
与圆 的两个交点关于直线
的两个交点关于直线 对称,则
对称,则 的首项为24,公差为
的首项为24,公差为 ,则当n=
时,该数列的前n项
,则当n=
时,该数列的前n项 取得最大值.
取得最大值.