题目内容
定义在R上的偶函数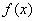 满足:对任意的
满足:对任意的 ,有
,有 .
.
则 ( )
A. B.
B.
C. D.
D.
A

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
题目内容
定义在R上的偶函数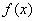 满足:对任意的
满足:对任意的 ,有
,有 .
.
则 ( )
A. B.
B.
C. D.
D.
A

 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案