题目内容
已知数列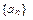 满足
满足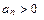 ,且对一切
,且对一切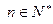 有
有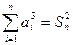 ,其中
,其中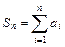 ,
,
(Ⅰ)求证对一切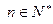 有
有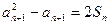 ,并求数列
,并求数列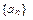 的通项公式;
的通项公式;
(Ⅱ)记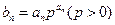 ,求数列
,求数列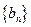 的前
的前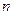 项和
项和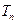 ;
;
(Ⅲ)求证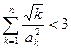 .
.
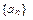 满足
满足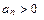 ,且对一切
,且对一切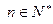 有
有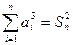 ,其中
,其中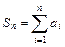 ,
, (Ⅰ)求证对一切
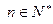 有
有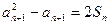 ,并求数列
,并求数列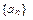 的通项公式;
的通项公式;(Ⅱ)记
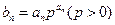 ,求数列
,求数列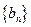 的前
的前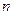 项和
项和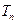 ;
;(Ⅲ)求证
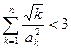 .
. (Ⅰ){ an}成等差数列,首项a1=1,公差d=1,故an=n;
(Ⅱ)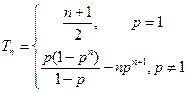 ;(Ⅲ)同解析。
;(Ⅲ)同解析。
(Ⅱ)
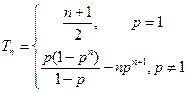 ;(Ⅲ)同解析。
;(Ⅲ)同解析。(Ⅰ)由ni=1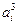 =Sn2, (1) 由n+1i=1
=Sn2, (1) 由n+1i=1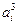 =Sn+12, (2)
=Sn+12, (2)
(2)-(1),得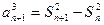 =(Sn+1+Sn)(Sn+1-Sn)=(2 Sn+an+1) an+1.
=(Sn+1+Sn)(Sn+1-Sn)=(2 Sn+an+1) an+1.
∵ an+1 >0,∴an+12-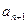 =2Sn.
=2Sn.
由an+12-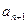 =2Sn,及an2-an =2Sn-1 (n≥2),
=2Sn,及an2-an =2Sn-1 (n≥2),
两式相减,得(an+1+ an)( an+1-an)= an+1+ an.
∵an+1+ an >0,∴an+1-an =1(n≥2)
当n=1,2时,易得a1=1,a2=2,∴an+1- an =1(n≥1).
∴{ an}成等差数列,首项a1=1,公差d=1,故an=n.
(Ⅱ)由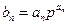 ,得
,得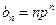 。所以
。所以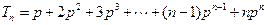 ,
,
当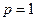 时,
时,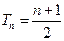 ;
;
当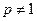 时,
时,
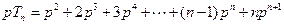 ,
,
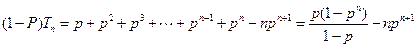
即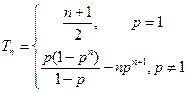
(Ⅲ)nk=1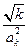 =nk=1
=nk=1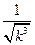 <1+nk=2
<1+nk=2
<1+nk=2=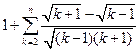
=1+nk=2 (-)
=1+1+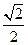 -
-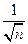 -<2+
-<2+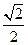 <3.
<3.
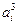 =Sn2, (1) 由n+1i=1
=Sn2, (1) 由n+1i=1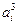 =Sn+12, (2)
=Sn+12, (2)(2)-(1),得
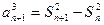 =(Sn+1+Sn)(Sn+1-Sn)=(2 Sn+an+1) an+1.
=(Sn+1+Sn)(Sn+1-Sn)=(2 Sn+an+1) an+1.∵ an+1 >0,∴an+12-
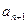 =2Sn.
=2Sn. 由an+12-
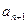 =2Sn,及an2-an =2Sn-1 (n≥2),
=2Sn,及an2-an =2Sn-1 (n≥2),两式相减,得(an+1+ an)( an+1-an)= an+1+ an.
∵an+1+ an >0,∴an+1-an =1(n≥2)
当n=1,2时,易得a1=1,a2=2,∴an+1- an =1(n≥1).
∴{ an}成等差数列,首项a1=1,公差d=1,故an=n.
(Ⅱ)由
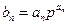 ,得
,得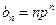 。所以
。所以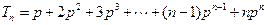 ,
,当
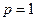 时,
时,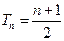 ;
;当
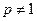 时,
时,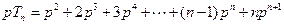 ,
,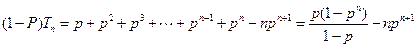
即
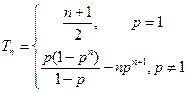
(Ⅲ)nk=1
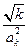 =nk=1
=nk=1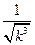 <1+nk=2
<1+nk=2 <1+nk=2=
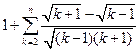
=1+nk=2 (-)
=1+1+
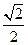 -
-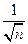 -<2+
-<2+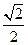 <3.
<3.
练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
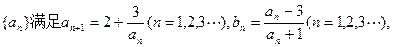
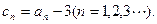
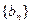 是等比数列;
是等比数列; 的通项公式;
的通项公式; ,证明数列{|
,证明数列{|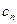 |}的前n项和Sn满足Sn<1.
|}的前n项和Sn满足Sn<1. 的前
的前 项的和
项的和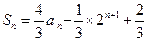 ,
,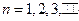
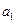 与通项
与通项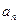 ;
;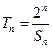 ,
,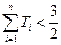 .
.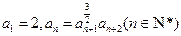 .
.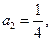 求a3,a4,并猜想a2008的值(不需证明);
求a3,a4,并猜想a2008的值(不需证明);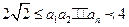 对n≥2恒成立,求a2的值。
对n≥2恒成立,求a2的值。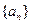 满足:
满足: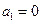 ,
,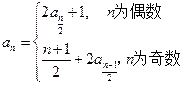
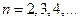
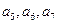 得值;
得值;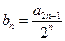 ,试求数列
,试求数列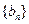 的通项公式;
的通项公式;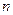 ,试讨论
,试讨论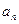 与
与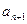 的大小关系。
的大小关系。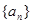 中,若
中,若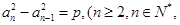
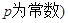 ,则称
,则称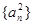 是等差数列;
是等差数列;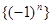 是等方差数列;
是等方差数列;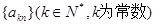 也是等方差数列;
也是等方差数列;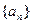 成等差数列,
成等差数列,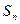 表示它的前
表示它的前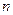 项和,且
项和,且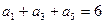 ,
,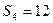 .
.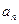 ;
;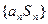 中,从第几项开始(含此项)以后各项均为负数?
中,从第几项开始(含此项)以后各项均为负数?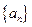 中,a1=8,a4=2且满足an+2=2an+1-an,(n∈N*)
中,a1=8,a4=2且满足an+2=2an+1-an,(n∈N*)
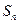 =|a1|+|a2|+…+|an|,求
=|a1|+|a2|+…+|an|,求