题目内容
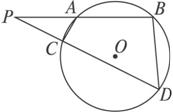
如图2-5-7,∠BAC的平分线与边BC和外接圆分别相交于D和E,延长AC交过D、E、C三点的圆于点F.
图2-5-7
（1）求证:EF2＝ED·EA;
（2）若AE＝6,EF＝3,求AF·AC的值.
思路解析:（1）要证EF2＝ED·EA,只需证△AEF∽△FED.（2）由于AC·AF＝AD·AE,而由（1）可求得DE,因而AD可以求出来,从而计算出AD·AE,即为AC·AF的值.
(1)证明:连结CE、DF.?
∵∠1＝∠2,∠3＝∠4,∠1＝∠3,∴∠2＝∠4.?
∵∠AEF＝∠FED,∴△AEF∽△FED.
∴
=
.∴EF2=ED·EA.
(2)解:由（1）知EF2＝AE·ED.?
∵EF =3,AE =6,∴
.∴
.?
∴AC·AF =AD·AE =
.
练习册系列答案
芒果教辅达标测试卷系列答案
相关题目
B
现有A、B两个班级,每个班级各有45名学生参加一次测验,每名参加者可获得0,1,2,3,4,5,6,7,8,9分这几种不同分值中的一种,A班的测试结果如下表所示：
分数 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
人数 | 1 | 3 | 5 | 7 | 6 | 8 | 6 | 4 | 3 | 2 |
B班的成绩如图2-2-16所示.
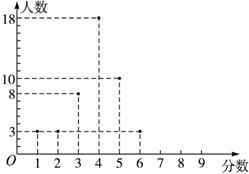
图2-2-16
(1)你认为哪个班级的成绩比较稳定？
(2)若两班共有60人及格,则参加者最少获得多少分才可能及格？
