题目内容
已知函数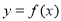 ,若在定义域内存在
,若在定义域内存在 ,使得
,使得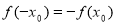 成立,则称
成立,则称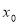 为函数
为函数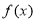 的局部对称点.
的局部对称点.
(1)若 、
、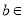 R且
R且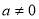 ,证明:函数
,证明:函数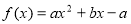 必有局部对称点;
必有局部对称点;
(2)若函数 在区间
在区间 内有局部对称点,求实数
内有局部对称点,求实数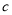 的取值范围;
的取值范围;
(3)若函数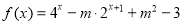 在R上有局部对称点,求实数
在R上有局部对称点,求实数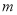 的取值范围.
的取值范围.
(1)详见解析;(2) 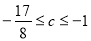 ;(3)
;(3) 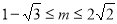
【解析】
试题分析:(1)由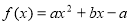 和
和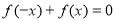 得到关于
得到关于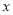 的方程
的方程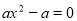 (
(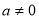 ),其中
),其中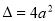 ,由于
,由于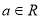 且
且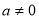 ,所以
,所以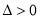 恒成立,所以函数
恒成立,所以函数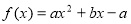 (
(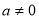 )必有局部对称点;(2)方程
)必有局部对称点;(2)方程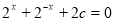 在区间
在区间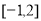 上有解,于是
上有解,于是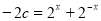 ,利用换元法,即可求出结果;(3)由于
,利用换元法,即可求出结果;(3)由于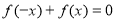 , 所以
, 所以 (*)在
(*)在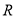 上有解,令
上有解,令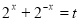 (
(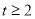 ),则
),则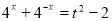 ,所以方程(*)变为
,所以方程(*)变为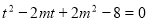 在区间
在区间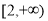 内有解,需满足条件:
内有解,需满足条件:
 ,解不等式,即可求出m的取值范围.
,解不等式,即可求出m的取值范围.
试题解析:【解析】
:(1)由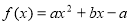 得
得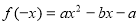 1分
1分
代入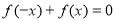 得,
得,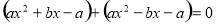 ,
,
得到关于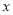 的方程
的方程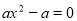 (
(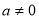 ),2分
),2分
其中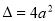 ,由于
,由于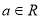 且
且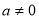 ,所以
,所以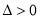 恒成立3分
恒成立3分
所以函数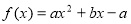 (
(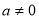 )必有局部对称点。4分
)必有局部对称点。4分
(2)方程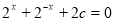 在区间
在区间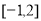 上有解,于是
上有解,于是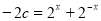 5分
5分
设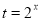 (
(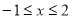 ),
), ,6分
,6分
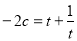 7分 其中
7分 其中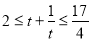 9分
9分
所以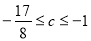 10分
10分
(3)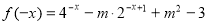 ,11分
,11分
由于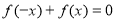 ,所以
,所以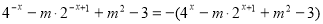 13分
13分
于是 (*)在
(*)在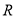 上有解14分
上有解14分
令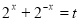 (
(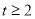 ),则
),则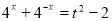 ,15分
,15分
所以方程(*)变为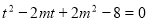 在区间
在区间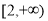 内有解,需满足条件:
内有解,需满足条件:
 16分
16分
即 ,化简得
,化简得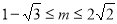 18分.
18分.
考点:1.新定义;2.换元法求函数的最值;3.恒成立问题.

练习册系列答案
相关题目
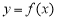 的定义域为
的定义域为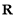 ,则“
,则“ ”是“函数
”是“函数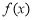 为奇函数”的( )
为奇函数”的( ) 的各项和等于公比
的各项和等于公比 ,则首项
,则首项 的取值范围是 .
的取值范围是 . 的解
的解 .
.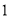 的正三角形
的正三角形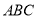 的边
的边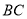 上有
上有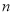 (
(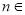 N*,
N*,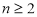 )等分点,沿向量
)等分点,沿向量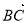 的方向依次为
的方向依次为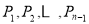 ,记
,记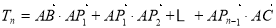 ,若给出四个数值:①
,若给出四个数值:①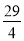 ②
②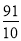 ③
③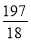 ④
④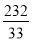 ,则
,则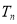 的值不可能的共有( )
的值不可能的共有( )
 中,三个内角
中,三个内角 、
、 、
、 的对边分别为
的对边分别为 、
、 、
、 ,若
,若 ,
, ,
, ,则
,则 .
. 的零点为
的零点为 的零点为
的零点为 ,若
,若 可以是
可以是 B.
B.
 D.
D.
 是等差数列,且
是等差数列,且 ,则
,则 的值为 .
的值为 .