题目内容
已知平面向量
,
,
满足:|
|=|
|=|
|=1,
•
=0,若
=x
+y
(x,y∈R),则x+y的最大值是
.
| OA |
| OB |
| OC |
| OA |
| OB |
| OC |
| OA |
| OB |
| OC |
| OA |
| OB |
| 2 |
| 2 |
分析:由已知将
=x
+y
两边平方后整理得x2+y2=1,进而根据基本不等式可得x+y的最大值
| OC |
| OA |
| OB |
解答:解:∵|
|=|
|=|
|=1,
•
=0,
将
=x
+y
两边平方得
2=x2
2+y2
2+2xy
•
,
所以 x2+y2=1,
由于 (x+y)2=x2+y2+2xy≤2(x2+y2)=2,
因此 x+y≤
,
即 x+y 最大值为
.
故答案为:
| OA |
| OB |
| OC |
| OA |
| OB |
将
| OC |
| OA |
| OB |
| OC |
| OA |
| OB |
| OA |
| OB |
所以 x2+y2=1,
由于 (x+y)2=x2+y2+2xy≤2(x2+y2)=2,
因此 x+y≤
| 2 |
即 x+y 最大值为
| 2 |
故答案为:
| 2 |
点评:本题考查的知识点是平面向量的基本定理,基本不等式,其中根据已知分析出x2+y2=1是解答的关键.

练习册系列答案
相关题目
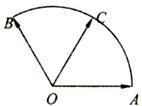 已知:如图,两个长度为1的平面向量
已知:如图,两个长度为1的平面向量