题目内容
对于自然数n(n≥2)的正整数次幂,可以如下分解为n个自然数的和的形式: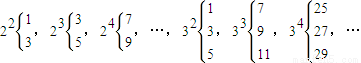
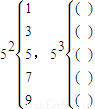 …仿此,53的分解中的最大数为 .
…仿此,53的分解中的最大数为 .
【答案】分析:本题考查的知识点是归纳推理,由:
 ,我们分析后易得:23可分解为2个连续的奇数,最小数为3;33可分解为3个连续的奇数,最小数为7…,则n3可分解为n个连续的奇数,最小数为n2-n+1,最大数为n2+n-1,由此易得53的分解中的最大数.
,我们分析后易得:23可分解为2个连续的奇数,最小数为3;33可分解为3个连续的奇数,最小数为7…,则n3可分解为n个连续的奇数,最小数为n2-n+1,最大数为n2+n-1,由此易得53的分解中的最大数.
解答:解:由已知得:
23可分解为2个连续的奇数,最小数为3;
33可分解为3个连续的奇数,最小数为7;
…,
则n3可分解为n个连续的奇数,
最小数为n2-n+1,
最大数为n2+n-1,
∴53的分解中的最大数为52+5-1=29.
故答案为:29
点评:归纳推理的一般步骤是:(1)通过观察个别情况发现某些相同性质;(2)从已知的相同性质中推出一个明确表达的一般性命题(猜想).

 ,我们分析后易得:23可分解为2个连续的奇数,最小数为3;33可分解为3个连续的奇数,最小数为7…,则n3可分解为n个连续的奇数,最小数为n2-n+1,最大数为n2+n-1,由此易得53的分解中的最大数.
,我们分析后易得:23可分解为2个连续的奇数,最小数为3;33可分解为3个连续的奇数,最小数为7…,则n3可分解为n个连续的奇数,最小数为n2-n+1,最大数为n2+n-1,由此易得53的分解中的最大数.解答:解:由已知得:
23可分解为2个连续的奇数,最小数为3;
33可分解为3个连续的奇数,最小数为7;
…,
则n3可分解为n个连续的奇数,
最小数为n2-n+1,
最大数为n2+n-1,
∴53的分解中的最大数为52+5-1=29.
故答案为:29
点评:归纳推理的一般步骤是:(1)通过观察个别情况发现某些相同性质;(2)从已知的相同性质中推出一个明确表达的一般性命题(猜想).

练习册系列答案
相关题目
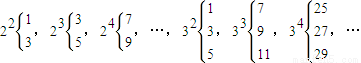
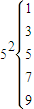 ,
,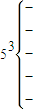 ,…
,…