题目内容
已知函数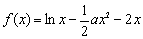 (
(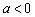 ).
).
(Ⅰ)若函数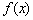 在定义域内单调递增,求实数
在定义域内单调递增,求实数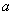 的取值范围;
的取值范围;
(Ⅱ)若 ,且关于
,且关于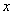 的方程
的方程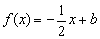 在
在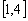 上恰有两个不等的实根,
上恰有两个不等的实根,
求实数 的取值范围;
的取值范围;
(Ⅲ)设各项为正数的数列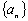 满足
满足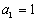 ,
,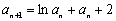 (
(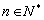 ),
),
求证: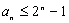 .
.
【解析】:(Ⅰ)函数的定义域为 ,
,
 ,依题意
,依题意 在
在 时恒成立,
时恒成立,
则 在
在 时恒成立,即
时恒成立,即 ,
,
当 时,
时, 取最小值-1,所以
取最小值-1,所以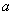 的取值范围是
的取值范围是 …………4分
…………4分
(Ⅱ) ,由
,由 得
得 在
在 上有两个不同的实根,
上有两个不同的实根,
设
 ,
, 时,
时, ,
, 时,
时,
 ,
, ,
,
 ,得
,得 则
则 ……9分
……9分
(Ⅲ)易证当 且
且 时,
时, .
.
由已知条件 ,
,
故 所以当
所以当 时,
时,

 ,
, 相乘得
相乘得 又
又 故
故 ,即
,即 ………14分
………14分

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
 中,已知内角A、B、C所对的边分别为
中,已知内角A、B、C所对的边分别为 ,向量
,向量 ,且向量
,且向量 .
. 的大小;
的大小; ,求
,求 的最大值.
的最大值.
 有极值点的概率为______________.______。
有极值点的概率为______________.______。
 为自然对数的底数)与
为自然对数的底数)与 的图象上存在关于
的图象上存在关于 B.
B. C.
C. D.
D.
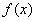 的定义域为D,若存在闭区间
的定义域为D,若存在闭区间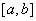
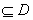 ,使得函数
,使得函数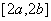 ,则称区间
,则称区间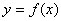 的“和谐区间”。下列函数中存在“和谐区间”的是 .
的“和谐区间”。下列函数中存在“和谐区间”的是 .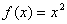 ,
, ②
②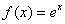 ,
,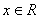
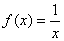 ,
, ④
④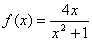 ,
, (
( 为虚数单位)在复平面内对应点的坐标是
为虚数单位)在复平面内对应点的坐标是 B.
B. C.
C. D.
D.
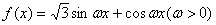 的图象与
的图象与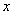 轴交点的横坐标构成一个公差为
轴交点的横坐标构成一个公差为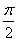 的等差数列,把函数
的等差数列,把函数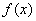 的图象沿
的图象沿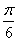 个单位,得到函数
个单位,得到函数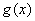 的图象.关于函数
的图象.关于函数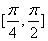 上是增函数 B. 其图象关于直线
上是增函数 B. 其图象关于直线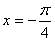 对称
对称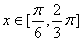 时,函数
时,函数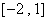
 B.
B. 
 D.
D. 
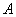 原料1千克、
原料1千克、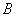 原料2千克;生产乙产品1桶需耗
原料2千克;生产乙产品1桶需耗