题目内容
19.已知椭圆${x^2}+\frac{y^2}{4}=1$和点$A({\frac{1}{2},\frac{1}{2}})$、$B({\frac{1}{2},1})$,若椭圆的某弦的中点在线段AB上,且此弦所在直线的斜率为k,则k的取值范围为( )| A. | [-4,-2] | B. | [-2,-1] | C. | [-4,-1] | D. | $[{-1,-\frac{1}{2}}]$ |
分析 由题意设出椭圆${x^2}+\frac{y^2}{4}=1$的某弦的两个端点分别为P(x1,y1),Q(x2,y2),中点为M(x0,y0),把P、Q的坐标代入椭圆方程,作差得到PQ的斜率与AB中点坐标的关系得答案.
解答 解:设椭圆${x^2}+\frac{y^2}{4}=1$的某弦的两个端点分别为P(x1,y1),Q(x2,y2),中点为M(x0,y0),
则${{x}_{1}}^{2}+\frac{{{y}_{1}}^{2}}{4}=1$,${{x}_{2}}^{2}+\frac{{{y}_{2}}^{2}}{4}=1$,
两式作差可得:${{x}_{1}}^{2}-{{x}_{2}}^{2}=-\frac{{{y}_{1}}^{2}}{4}+\frac{{{y}_{2}}^{2}}{4}$,
即$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}=-\frac{4({x}_{1}+{x}_{2})}{{y}_{1}+{y}_{2}}=-\frac{4{x}_{0}}{{y}_{0}}$=$-\frac{4×\frac{1}{2}}{{y}_{0}}=-\frac{2}{{y}_{0}}$,
由题意可知,$\frac{1}{2}≤$y0≤1,
∴k=$-\frac{2}{{y}_{0}}$($\frac{1}{2}≤$y0≤1),则k∈[-4,-2].
故选:A.
点评 本题考查椭圆的简单性质,训练了“中点弦”问题的求解方法,属中档题.

练习册系列答案
相关题目
7.已知函数f(x)是定义域R在上的奇函数,且在区间[0,+∞)单调递增,若实数a满足f(log2a)+f(log2$\frac{1}{a}$)≤2f(1),则a的取值范围是( )
| A. | (-∞,2] | B. | $({0,\frac{1}{2}}]$ | C. | $[{\frac{1}{2},2}]$ | D. | (0,2] |
11.由1,2,3这三个数字组成的没有重复数字的三位自然数共有( )
| A. | 6个 | B. | 8个 | C. | 12个 | D. | 15个 |
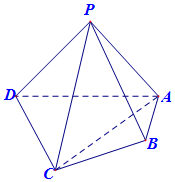 如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,PA⊥PD,PA=PD,AB⊥AD,AB=1,AD=2,AC=CD=$\sqrt{5}$.
如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,PA⊥PD,PA=PD,AB⊥AD,AB=1,AD=2,AC=CD=$\sqrt{5}$.