题目内容
证明：在区间[1，+∞）上，函数f（x）=-2x2+4x-3是单调递减的．
分析：求导可得f′（x）=-4x+4，令其小于0，可得单调递减区间．
解答：解：∵f（x）=-2x2+4x-3，
∴其导数f′（x）=-4x+4，
令-4x+4＜0，解得x＞1，
故函数的单调递减区间为[1，+∞），
故原命题得证
∴其导数f′（x）=-4x+4，
令-4x+4＜0，解得x＞1，
故函数的单调递减区间为[1，+∞），
故原命题得证
点评：本题考查函数单调性的判断与证明，转化为导数的正负是解决问题的关键，属基础题．
练习册系列答案
相关题目
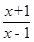，求函数φ (x)的单调区间；
，求函数φ (x)的单调区间；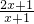
．