题目内容
函数f(x)=
ax3+ax2+x+1有极值的充要条件是（ ）
| 1 |
| 3 |
| A、a≥1或a≤0 |
| B、、a＞1或a＜0 |
| C、a≥1或a＜0 |
| D、0＜a＜1 |
分析：将函数f（x）有极值转化成f′（x）有两不等的根，再利用判别式进行判定即可．
解答：解：函数f(x)=
ax3+ax2+x+1有极值
则f′（x）=ax2+2ax+1=0有两不等的根
当a=0时，无解
当a≠0时，△＞0．即4a2-4a＞0
解得a＞1或a＜0，
故选B．
| 1 |
| 3 |
则f′（x）=ax2+2ax+1=0有两不等的根
当a=0时，无解
当a≠0时，△＞0．即4a2-4a＞0
解得a＞1或a＜0，
故选B．
点评：本题主要考查了利用导数研究函数的极值，以及充要条件的判断，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
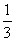(m∈R,e=2.718 28…是自然对数的底数).
.
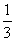(m∈R,e=2.718 28…是自然对数的底数).
.