题目内容
(本小题满分12分)在如图所示的多面体中,底面△ABC是边长为2的正三角形,DA和EC均垂直于平面ABC,且DA = 2,EC = 1.
(Ⅰ)求点A到平面BDE的距离;
(Ⅱ)求二面角B–ED–A的正切值.
(Ⅰ)求点A到平面BDE的距离;
(Ⅱ)求二面角B–ED–A的正切值.
 ,
,
(Ⅰ)∵DE = BE =
 ,BD =
,BD = ,
,∴S△BDE =
 ,设点A到平面BDE的距离为h.
,设点A到平面BDE的距离为h.又∵S△ABC =
 ,VB–ADE = VA–BDE
,VB–ADE = VA–BDE∴
 ∴h =
∴h =
即点A到平面BDE的距离为
 . ……6分
. ……6分(Ⅱ)∵DA⊥平面ABC,∴平面DACE⊥平面ABC
取AC的中点M,连结BM,则BM⊥AC,BM⊥平面DACE.
过M作MN⊥DE,交DE于N,连结BN,则BN⊥DE,
∴∠BNM是所求二面角的平面角.
设AC、DE的延长线相交于点P,∵DA = 2EC,∴CP = 2
 由△MNP∽△DAP得
由△MNP∽△DAP得 ,MP = 3,DA = 2
,MP = 3,DA = 2DP =
 ,∴MN =
,∴MN =
又∵BM =
 ,∴tan∠BNM =
,∴tan∠BNM = . ……12分
. ……12分
练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
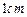 的正方体。
的正方体。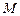 、
、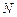 、
、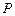 、
、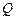 重合,则可以围成怎样的几何体?请求出此几何体的体积;
重合,则可以围成怎样的几何体?请求出此几何体的体积; 体?请按图乙中所标字母写出这几个几何体的名称;
体?请按图乙中所标字母写出这几个几何体的名称;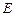 为棱
为棱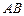 上的动点,试判断
上的动点,试判断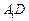 与平面
与平面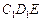 是否垂直,并说明理由。
是否垂直,并说明理由。
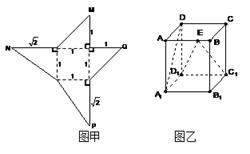
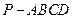 的三视图如下图所示,其中主视图、侧视图是直角三角形,俯视图是有一条对角线的正方形.
的三视图如下图所示,其中主视图、侧视图是直角三角形,俯视图是有一条对角线的正方形.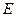 是侧棱
是侧棱 上的动点.
上的动点.
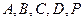 在同一球面上,求该球的体积.
在同一球面上,求该球的体积.
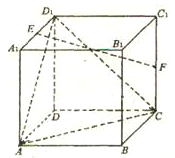
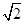 ,四个顶点在同一个球面上,则此球的表面积为
,四个顶点在同一个球面上,则此球的表面积为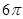
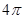
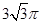
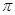
 ,底面
,底面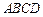 为矩形,侧棱
为矩形,侧棱 ,其中
,其中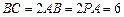 ,
,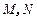 为侧棱
为侧棱 上的两个三等分点,如图所示.
上的两个三等分点,如图所示.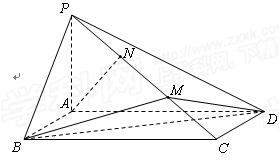
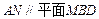 ;
;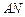 与
与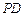 所成角的余弦值;
所成角的余弦值;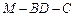 的余弦值.
的余弦值. )
)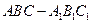 的底面边长是
的底面边长是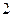 ,
, 、E是
、E是 、BC的中点,AE=DE
、BC的中点,AE=DE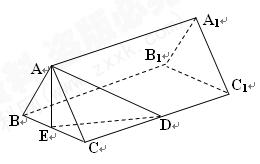
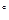 ,在四边形ABCD中,∠ADC=∠DAB=90
,在四边形ABCD中,∠ADC=∠DAB=90
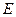 在棱
在棱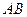 上,
上,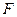 在棱
在棱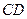 上.并且
上.并且 (0<l<+∞),设a为异面直线
(0<l<+∞),设a为异面直线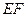 与
与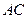 所成的角,b 为异面直线EF与BD所成的角,则a+b的值是
所成的角,b 为异面直线EF与BD所成的角,则a+b的值是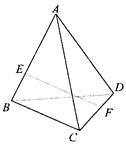
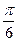
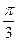
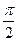
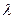 的值有关
的值有关