题目内容

12．已知示数x，y满足$\left\{\begin{array}{l}{x+y≥0}\\{x-y+2≥0}\\{2x+y-4≤0}\end{array}\right.$，则目标函数z=3x+y的最大值和最小值分别是（　　）
A．6，-2B．8，-2C．6，-4D．8，-4

分析 先画出满足条件的平面区域，求出A，B的坐标，将z=3x+y变形为y=-3x+z，平移直线从而求出z的最大值和最小值．

解答 解：画出满足条件的平面区域，如图示：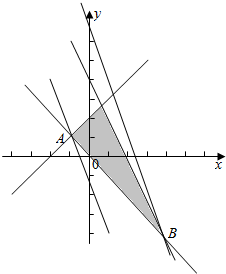
，
由z=3x+y得：y=-3x+z，
显然直线y=-3x+z过A点时，z最小，
直线y=-3x+z过B点时，z最大，
由$\left\{\begin{array}{l}{x-y+2=0}\\{x+y=0}\end{array}\right.$，解得A（-1，1），
由$\left\{\begin{array}{l}{x+y=0}\\{2x+y-4=0}\end{array}\right.$，解得：B（4，-4），
将A（-1，1）代入y=-3x+z得：z=-2，
将B（4，-4）代入y=-3x+z得：z=8，
故选：B．

点评 本题考查了简单的线性规划问题，考查数形结合思想，是一道基础题．

练习册系列答案
相关题目
2．函数y=$\sqrt{3-4x+{x}^{2}}$的定义域为M．
（1）求M和函数的值域；
（2）当x∈M时，关于x的方程4x-2×2x=b（b∈R）有两个不等实数根，求b的取值范围．
3．方程x|x|-y|y|=-1的曲线即为函数y=f（x）的图象，对于函数y=f（x），有如下结论：
①f（x）在R上单调递减；
②函数F（x）=f（x）-x-$\sqrt{2}$存在3个零点；
③函数y=f（x）的值域是R；
④函数g（x）和f（x）的图象关于原点对称，则函数y=g（x）的图象就是方程x|x|-y|y|=1确定的曲线．
其中所有正确的命题序号是②③④．
20．已知在等差数列{an}中，a1=4，${a}_{3}=\frac{28}{5}$，则数列{an}的前6项和等于（　　）
A．70B．36C．32D．30
7．已知a，b为非零实数，且a＞b，则下列命题成立的是（　　）
A．a2＞b2B．|a|＞|b|C．（$\frac{1}{2}$）a＜（$\frac{1}{2}$）bD．$\frac{b}{a}＜1$
17．已知a＞b，则下列结论正确的是（　　）
A．ac＞bcB．$\frac{1}{a}＞\frac{1}{b}$C．a2＞b2D．a+c＞b+c
4．已知Sn为等差数列{an}的前n项和，a4=4，S5=15．
（1）求数列{an}的通项公式；
（2）若等比数列{bn}满足b1=a1，b4=a27，Tn为数列{bn}的前n项和，且Tn=40．求n的值．
1．在一次抽样调查中，获得一组具有线性关系的数据（xi，yi），i=1，2，…，10，用最小二乘法得到的线性回归方程为y=$\widehat{a}$x+2，若这组数据的样本点中心为（3，4），则$\widehat{a}$=$\frac{2}{3}$．
8．已知$f（x）=2cosxsin（x+\frac{π}{3}）-\sqrt{3}{sin^2}x+sinxcosx+1$
①求函数f（x）的最小正周期和函数的单调增区间；
②当$x∈[0，\frac{5}{12}π]$时，求函数f（x）的值域．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网