题目内容
如图所示,PDCE为矩形,ABCD为梯形,平面PDCE⊥平面ABCD,
∠BAD=∠ADC=90°,AB=AD=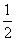 CD=1,PD=
CD=1,PD=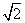 .
.
(1)若M为PA中点,求证:AC∥平面MDE;
(2)在线段PC上是否存在一点Q(除去端点),使得平面QAD与平面PBC所成锐二面角的大小为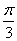 。
。
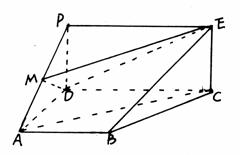
(1)证明:在矩形PDCE中,连接PC交DE于点N,则点N为PC的中点,在ΔAPC 中,点M为PA的中点,点N为PC的中点,∴AC∥MN,
又 平面MDE,
平面MDE, 平面MDE。
平面MDE。



 (2)设CQ=
(2)设CQ= CP,得Q(0,2-
CP,得Q(0,2- )
)


故在PC上存在点Q满足条件,

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 成立的所有常数
成立的所有常数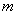 中,我们把
中,我们把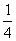 叫做
叫做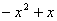 的上确界,若
的上确界,若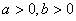 ,且
,且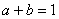 ,则
,则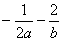 的上确界是
的上确界是  的圆
的圆 中,
中, ,
, 为
为 的中点,
的中点, 的延长线交圆
的延长线交圆 ,则线段
,则线段 的长为 .
的长为 .
 C.48+8
C.48+8
 :
: 与
与 :
: 的交点为
的交点为 .
. :
: 的直线方程;
的直线方程; 的图象沿
的图象沿 轴向左平移
轴向左平移 个单位后,得到一个偶函数的图象,则
个单位后,得到一个偶函数的图象,则 的一个可能取值为( )
的一个可能取值为( ) B.
B.  C.0 D.
C.0 D. 
 中,
中, ,
,
 ,过
,过 作
作 ,
, ,
, 与外接圆交于点
与外接圆交于点 ,则
,则 的长为
的长为

 时,函数
时,函数 取得最大值,则
取得最大值,则 ______
______ 上至少有三个不同的点到直线
上至少有三个不同的点到直线 的距离为
的距离为 ,则直线
,则直线 的倾斜角的取值范围是( )
的倾斜角的取值范围是( ) B.
B. C.
C. D.
D.