题目内容
设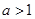 ,若函数
,若函数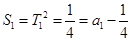 在区间
在区间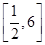 上是增函数,则
上是增函数,则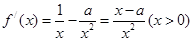 的取值范围是 .
的取值范围是 .
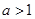 ,若函数
,若函数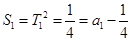 在区间
在区间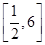 上是增函数,则
上是增函数,则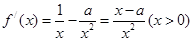 的取值范围是 .
的取值范围是 .
试题分析:根据题意,由于函数
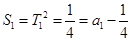 在区间
在区间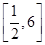 上是增函数,则说明其导数恒大与等于零,即
上是增函数,则说明其导数恒大与等于零,即 ,故可知
,故可知
点评:主要是考查了函数的单调性,以及导数于函数单调性关系的 运用,属于基础题。

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
题目内容
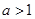 ,若函数
,若函数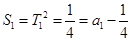 在区间
在区间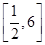 上是增函数,则
上是增函数,则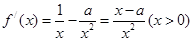 的取值范围是 .
的取值范围是 .
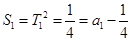 在区间
在区间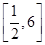 上是增函数,则说明其导数恒大与等于零,即
上是增函数,则说明其导数恒大与等于零,即 ,故可知
,故可知

 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案