题目内容
16.方程(x+$\frac{a}{b}$$\sqrt{{b}^{2}-{y}^{2}}$)2+(y-$\frac{b}{a}$$\sqrt{{a}^{2}-{x}^{2}}$)2=0所表示的曲线的图形是( )| A. |  | B. | 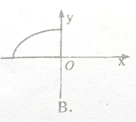 | C. |  | D. |  |
分析 将方程等价变形,即可得出结论
解答 解:由(x+$\frac{a}{b}$$\sqrt{{b}^{2}-{y}^{2}}$)2+(y-$\frac{b}{a}$$\sqrt{{a}^{2}-{x}^{2}}$)2=0,得x=-$\frac{a}{b}$$\sqrt{{b}^{2}-{y}^{2}}$且y=$\frac{b}{a}$$\sqrt{{a}^{2}-{x}^{2}}$.
∴ab>0,方程(x+$\frac{a}{b}$$\sqrt{{b}^{2}-{y}^{2}}$)2+(y-$\frac{b}{a}$$\sqrt{{a}^{2}-{x}^{2}}$)2=0表示椭圆在第二象限的部分,
ab<0,则x>0,y<0,无选项.
故选:B
点评 本题考查轨迹方程,考查学生分析解决问题的能力,属于基础题.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
18. 如图所示,在平面直角坐标系xOy中,点B,C分别在x轴和y轴非负半轴上,点A在第一象限,且∠BAC=90°,AB=AC=4,那么O,A两点间距离的( )
如图所示,在平面直角坐标系xOy中,点B,C分别在x轴和y轴非负半轴上,点A在第一象限,且∠BAC=90°,AB=AC=4,那么O,A两点间距离的( )
 如图所示,在平面直角坐标系xOy中,点B,C分别在x轴和y轴非负半轴上,点A在第一象限,且∠BAC=90°,AB=AC=4,那么O,A两点间距离的( )
如图所示,在平面直角坐标系xOy中,点B,C分别在x轴和y轴非负半轴上,点A在第一象限,且∠BAC=90°,AB=AC=4,那么O,A两点间距离的( )| A. | 最大值是$4\sqrt{2}$,最小值是4 | B. | 最大值是8,最小值是4 | ||
| C. | 最大值是$4\sqrt{2}$,最小值是2 | D. | 最大值是8,最小值是2 |
 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)左右焦点,上下顶点依次为F1,F2,B1,B2,若四边形F1B1F2B2的面积为8,且椭圆的离心率为$\frac{\sqrt{2}}{2}$.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)左右焦点,上下顶点依次为F1,F2,B1,B2,若四边形F1B1F2B2的面积为8,且椭圆的离心率为$\frac{\sqrt{2}}{2}$.