题目内容
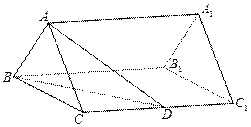 如图,正三棱柱ABC-A1B1C1的底面边长是2,D是侧棱CC1的中点,直线AD与侧面BB1C1C所成的角为45°.
如图,正三棱柱ABC-A1B1C1的底面边长是2,D是侧棱CC1的中点,直线AD与侧面BB1C1C所成的角为45°.小题1:求此正三棱柱的侧棱长;
小题2:求二面角A-BD-C的大小;
小题3:求点C到平面ABD的距离.
小题1:设正三棱柱
 —
— 的侧棱长为
的侧棱长为 .取
.取 中点
中点 ,连
,连 .
.
 是正三角形,
是正三角形, .
.又底面
 侧面
侧面 ,且交线为
,且交线为 .
. 侧面
侧面 .
.连
 ,则直线
,则直线 与侧面
与侧面 所成的角
所成的角为
 .
. 在
 中,
中, ,解得
,解得 .
.  此正三棱柱的侧棱长为
此正三棱柱的侧棱长为 . ……………………5分
. ……………………5分注:也可用向量法求侧棱长.
小题2:
过
 作
作 于
于 ,连
,连 ,
, 侧面
侧面

 .
. 为二面角
为二面角 的平面角.
的平面角. 在
 中,
中, ,又
,又 ,
, 
 .
.又

 在
在 中,
中, .
. 故二面角
 的大小为
的大小为
小题3:
由(Ⅱ)可知,
 平面
平面 ,
, 平面
平面 平面
平面 ,且交线为
,且交线为 ,
, 过
过 作
作 于
于 ,则
,则 平面
平面 .
. 在
 中,
中, .
. 
 为
为 中点,
中点, 点
点 到平面
到平面 的距离为
的距离为 . …………14分
. …………14分同答案

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
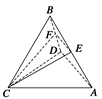 (1)直线EF∥平面ACD;
(1)直线EF∥平面ACD;
 ,
, ,
,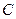 三点都是平面
三点都是平面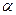 与平面
与平面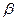 的公共点,并且
的公共点,并且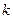 个四面体,则
个四面体,则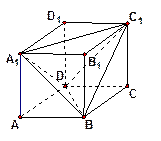
 2AB,
2AB,  中,
中, ,
,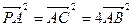 .
.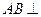 平面
平面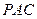 ;
;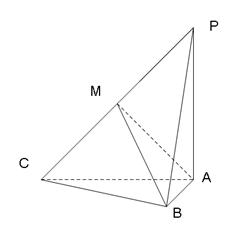 (Ⅱ)若
(Ⅱ)若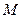 为线段
为线段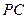 上的点,设
上的点,设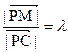 ,问
,问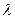 为何值时能使
为何值时能使 平面
平面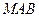 ;
;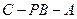 的大小.
的大小. cm
cm )?
)?