Question

【题目】集合，，.若集合中的所有元素都能用中不超过9个的不同元素相加表示，求，并构造达到最小时对应的一个集合.

Answer 1

【答案】，为满足条件的集合.

【解析】

设.

依题意应有.

注意到，，

，

.

故.

下面证明：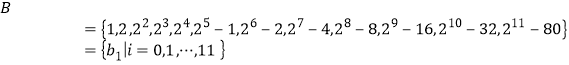

满足条件.

1.首先用数学归纳法证明：对任意的，可以表示成中至多个不同元素之和.

当时，对任意的，由二进制知识知

.

其中，或1，不全为1，.

即可表示成中至多4个不同元素之和.

假设时，命题成立.

当时，由归纳假设易知，当时命题成立；当时，.

由归纳假设，可以表示成中至多个不同元素之和，故可以表示成中至多个不同元素之和.

2.对，取，使得.

若，则，矛盾.

若，则，同1知可表示成中至多3个不同元素之和.故可表示成中至多9个不同元素之和.

若则，由1知可表示成中至多个不同元素之和.故可表示成中至多个不同元素之和.

3.对，则.

取，使得，从而，.

由1知可表示成中至多个不同元素之和.

故可表成中至多个不同元素之和.

综上，，为满足条件的集合.