题目内容
【题目】将平面上每个点染为![]() 种颜色之一,同时满足:
种颜色之一,同时满足:
(1)每种颜色的点都有无穷多个,且不全在同一条直线上;
(2)至少有一条直线上所有的点恰为两种颜色.
求![]() 的最小值,使得存在互不同色的四个点共圆.
的最小值,使得存在互不同色的四个点共圆.
【答案】5
【解析】
由已知![]() .
.
若![]() ,在平面上取一定圆
,在平面上取一定圆![]() 及上面三点
及上面三点![]() 、
、![]() 、
、![]() ,将弧
,将弧![]() (含点
(含点![]() 不含
不含![]() )、弧
)、弧![]() (含点
(含点![]() 不含
不含![]() )、弧
)、弧![]() (含点
(含点![]() 不含
不含![]() )分别染为1、2、3色,平面上其他点染为4色,则满足题意且不存在四个互不同色的点共圆.
)分别染为1、2、3色,平面上其他点染为4色,则满足题意且不存在四个互不同色的点共圆.
所以,![]() .
.
当![]() 时,假设不存在四个互不同色的点共圆.由条件(2)知,存在直线
时,假设不存在四个互不同色的点共圆.由条件(2)知,存在直线![]() 上恰有两种颜色的点(设
上恰有两种颜色的点(设![]() 上仅有颜色1、2的点),再由条件(1)知,存在颜色分别为3、4、5的点
上仅有颜色1、2的点),再由条件(1)知,存在颜色分别为3、4、5的点![]() 、
、![]() 、
、![]() 不共线,设过
不共线,设过![]() 、
、![]() 、
、![]() 的圆为
的圆为![]() (如图).
(如图).
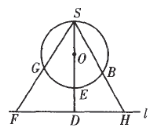
若![]() 与
与![]() 有公共点,则存在四个互不同色的点共圆,矛盾.
有公共点,则存在四个互不同色的点共圆,矛盾.
若![]() 与
与![]() 相离,则过点
相离,则过点![]() 作
作![]() 的垂线与
的垂线与![]() 交于点
交于点![]() .
.
设![]() 的颜色为1,垂线与
的颜色为1,垂线与![]() 交于点
交于点![]() 、
、![]() ,如图3.
,如图3.
设![]() 的颜色为3.考虑
的颜色为3.考虑![]() 上颜色为2的点
上颜色为2的点![]() ,
,![]() 与
与![]() 交于点
交于点![]() .
.
因为![]() ,所以,
,所以,![]() 、
、![]() 、
、![]() 、
、![]() 四点共圆.则
四点共圆.则![]() 只能为3色.
只能为3色.
又![]() 、
、![]() 必有一点不同于
必有一点不同于![]() (设为
(设为![]() ),
),![]() 与
与![]() 交于点
交于点![]() .
.
因为![]() ,所以,
,所以,![]() 、
、![]() 、
、![]() 、
、![]() 四点共圆.则
四点共圆.则![]() 只能为1色.
只能为1色.
故![]() .
.
从而,![]() 、
、![]() 、
、![]() 、
、![]() 四点共圆,且互不同色,矛盾.
四点共圆,且互不同色,矛盾.
所以,当![]() 时,存在四个互不同色的点共圆.
时,存在四个互不同色的点共圆.
因此,![]() 的最小值是5.
的最小值是5.

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案
相关题目