题目内容
（本题满分12分）已知
是定义在
上的奇函数，且当
时，
．
（1）求在
上的解析式；
(2) 证明在
上是减函数；
（3）当
取何值时，
在
上有解．
解：设
则
…… 1 分
∴ 
…… 2 分
∵ 为奇函数 ∴
∴
…… 3 分
又 
∴ 
…… 4 分
综上：
…… 5 分
（2）（解法一）证明：设
则
-
=
…… 7 分
∵ ∴
，
∴
又
∴
，
∴在
上是减函数. ……
9 分
（解法二）证明：∵
……7 分
∵
∴ 
即
又 
∴ 
∴在上是减函数. …… 9 分
(3) 是定义在上的奇函数，且由（2）知，在上单调递减
∴ 在
上单调递减，
∴当
时，有
即
…… 11 分
∴要使方程在上有解，只需
. 故
.… 12 分
解析
练习册系列答案
口算心算速算应用题系列答案
同步拓展阅读系列答案
相关题目
.
的范围，使
在区间
上是单调函数。 （2）求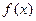
的最小值。
的定义域为A,
(
<1) 的定义域为B.
A, 求实数
[0, 1]，总有f（x）≥0; 
, n
是定义在（1，4）上单调递减函数，且
，求
的取值范围。
为奇函数,当
时, 
的最小值为2.
,求证:
且
,求证:
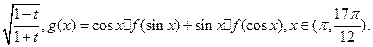
3且对任意x，y∈R都有f(x+y)=f(x)+f(y)．(1)求证f(x)为奇函数；(2)若f(k·3
)+f(3
的最大值．