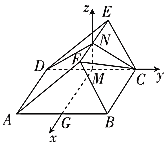
题目内容
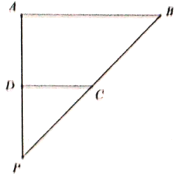
【题目】如图1,在等腰梯形![]() 中,两腰
中,两腰![]() ,底边
,底边![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 的三等分点,
的三等分点,![]() 是
是![]() 的中点.分别沿
的中点.分别沿![]() ,
,![]() 将四边形
将四边形![]() 和
和![]() 折起,使
折起,使![]() ,
,![]() 重合于点
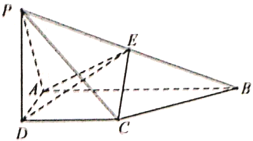
重合于点![]() ,得到如图2所示的几何体.在图2中,
,得到如图2所示的几何体.在图2中,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点.
的中点.
(1)证明:![]() 平面
平面![]() .
.
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)证明见解析 (2)![]()
【解析】
(1)先证![]() ,再证
,再证![]() ,由
,由![]() 可得
可得![]() 平面
平面![]() ,从而推出
,从而推出![]() 平面
平面![]() ;(2) 建立空间直角坐标系,求出平面
;(2) 建立空间直角坐标系,求出平面![]() 的法向量与
的法向量与![]() ,坐标代入线面角的正弦值公式即可得解.
,坐标代入线面角的正弦值公式即可得解.
(1)证明:连接![]() ,
,![]() ,由图1知,四边形
,由图1知,四边形![]() 为菱形,且
为菱形,且![]() ,
,
所以![]() 是正三角形,从而
是正三角形,从而![]() .
.
同理可证,![]() ,
,
所以![]() 平面
平面![]() .
.
又![]() ,所以
,所以![]() 平面
平面![]() ,
,
因为![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]() .
.
易知![]() ,且
,且![]() 为
为![]() 的中点,所以
的中点,所以![]() ,
,
所以![]() 平面
平面![]() .
.
(2)解:由(1)可知![]() ,
,![]() ,且四边形
,且四边形![]() 为正方形.设
为正方形.设![]() 的中点为
的中点为![]() ,
,
以![]() 为原点,以
为原点,以![]() ,
,![]() ,
,![]() 所在直线分别为
所在直线分别为![]() ,
,![]() ,
,![]() 轴,建立空间直角坐标系
轴,建立空间直角坐标系![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
由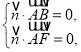 得
得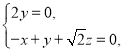
取![]() .
.
设直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,
,
所以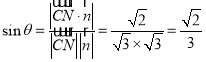 ,
,
所以直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】去年年底,某商业集团公司根据相关评分细则,对其所属25家商业连锁店进行了考核评估.将各连锁店的评估分数按[60,70), [70,80), [80,90), [90,100),分成四组,其频率分布直方图如下图所示,集团公司依据评估得分,将这些连锁店划分为A,B,C,D四个等级,等级评定标准如下表所示.
评估得分 | [60,70) | [70,80) | [80,90) | [90,100) |
评定等级 | D | C | B | A |

(1)估计该商业集团各连锁店评估得分的众数和平均数;
(2)从评估分数不小于80分的连锁店中任选2家介绍营销经验,求至少选一家A等级的概率.