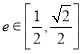题目内容
【题目】设![]() ,
,![]() ,其中a,
,其中a,![]() .
.
![]() Ⅰ
Ⅰ![]() 求
求![]() 的极大值;
的极大值;
![]() Ⅱ
Ⅱ![]() 设
设![]() ,
,![]() ,若
,若![]() 对任意的
对任意的![]() ,
,![]() 恒成立,求a的最大值;
恒成立,求a的最大值;
![]() Ⅲ
Ⅲ![]() 设
设![]() ,若对任意给定的
,若对任意给定的![]() ,在区间
,在区间![]() 上总存在s,
上总存在s,![]() ,使
,使![]() 成立,求b的取值范围.
成立,求b的取值范围.
【答案】(Ⅰ)1;(Ⅱ)![]() ;(Ⅲ)
;(Ⅲ)![]() .
.
【解析】
![]() Ⅰ
Ⅰ![]() 求出
求出![]() 的导数,令导数大于0,得增区间,令导数小于0,得减区间,进而求得
的导数,令导数大于0,得增区间,令导数小于0,得减区间,进而求得![]() 的极大值;
的极大值;
![]() Ⅱ
Ⅱ![]() 当
当![]() ,
,![]() 时,求出
时,求出![]() 的导数,以及
的导数,以及![]() 的导数,判断单调性,去掉绝对值可得
的导数,判断单调性,去掉绝对值可得![]() ,构造函数
,构造函数![]() ,求得
,求得![]() 的导数,通过分离参数,求出右边的最小值,即可得到a的范围;
的导数,通过分离参数,求出右边的最小值,即可得到a的范围;
![]() Ⅲ
Ⅲ![]() 求出
求出![]() 的导数,通过单调区间可得函数
的导数,通过单调区间可得函数![]() 在
在![]() 上的值域为
上的值域为![]() ,由题意分析
,由题意分析![]() 时,结合
时,结合![]() 的导数得到
的导数得到![]() 在区间
在区间![]() 上不单调,所以,
上不单调,所以,![]() ,再由导数求得
,再由导数求得![]() 的最小值,即可得到所求范围.
的最小值,即可得到所求范围.
![]() Ⅰ
Ⅰ![]() ,
,
当![]() 时,
时,![]() ,
,![]() 在
在![]() 递增;当
递增;当![]() 时,
时,![]() ,
,![]() 在
在![]() 递减.
递减.
则有![]() 的极大值为
的极大值为![]() ;
;
![]() Ⅱ
Ⅱ![]() 当
当![]() ,
,![]() 时,
时,![]() ,
,![]() ,
,
![]() 在
在![]() 恒成立,
恒成立,![]() 在
在![]() 递增;
递增;
由![]() ,
,![]() 在
在![]() 恒成立,
恒成立,![]() 在
在![]() 递增.
递增.
设![]() ,原不等式等价为
,原不等式等价为![]() ,
,
即![]() ,
,![]() ,
,![]() 在
在![]() 递减,
递减,
又![]() ,
,![]() 在
在![]() 恒成立,
恒成立,
故![]() 在
在![]() 递增,
递增,![]() ,
,
令![]() ,
,![]() ,
,
∴![]()
![]() ,
,![]() 在
在![]() 递增,
递增,
即有![]() ,即
,即![]() ;
;
![]() Ⅲ
Ⅲ![]() ,
,
当![]() 时,
时,![]() ,函数
,函数![]() 单调递增;
单调递增;
当![]() 时,
时,![]() ,函数
,函数![]() 单调递减.
单调递减.
又因为![]() ,
,![]() ,
,![]() ,
,
所以,函数![]() 在
在![]() 上的值域为
上的值域为![]() .
.
由题意,当![]() 取
取![]() 的每一个值时,
的每一个值时,
在区间![]() 上存在
上存在![]() ,
,![]() 与该值对应.
与该值对应.
![]() 时,
时,![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,
,![]() 单调递减,不合题意,
单调递减,不合题意,
当![]() 时,
时,![]() 时,
时,![]() ,
,
由题意,![]() 在区间
在区间![]() 上不单调,所以,
上不单调,所以,![]() ,
,
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() 0'/>
0'/>
所以,当![]() 时,
时,![]() ,
,
由题意,只需满足以下三个条件:![]() ,
,
![]() ,
,![]() 使
使![]() .
.
![]() ,所以
,所以![]() 成立
成立![]() 由
由![]() ,所以
,所以![]() 满足,
满足,
所以当b满足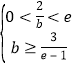 即
即![]() 时,符合题意,
时,符合题意,
故b的取值范围为![]() .
.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目