题目内容
【题目】已知点
是抛物线
的准线上一点，F为抛物线的焦点，P为抛物线上的点，且
，若双曲线C中心在原点，F是它的一个焦点，且过P点，当m取最小值时，双曲线C的离心率为______.
【答案】
【解析】
由点
坐标可确定抛物线方程，由此得到
坐标和准线方程；过
作准线的垂线，垂足为
，根据抛物线定义可得
，可知当直线
与抛物线相切时，
取得最小值；利用抛物线切线的求解方法可求得点坐标，根据双曲线定义得到实轴长，结合焦距可求得所求的离心率.
是抛物线
准线上的一点 
抛物线方程为
，准线方程为
过作准线的垂线，垂足为，则
设直线的倾斜角为
，则
当取得最小值时，
最小，此时直线与抛物线相切
设直线
的方程为
，代入得：
，解得：
或
双曲线的实轴长为
，焦距为
双曲线的离心率
故答案为：
练习册系列答案
相关题目
【题目】为了调查一款手机的使用时间，研究人员对该款手机进行了相应的测试，将得到的数据统计如下图所示：
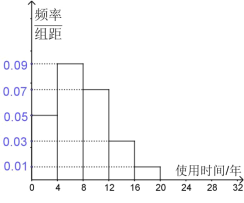
并对不同年龄层的市民对这款手机的购买意愿作出调查，得到的数据如下表所示：
愿意购买该款手机 | 不愿意购买该款手机 | 总计 | |
40岁以下 | 600 | ||
40岁以上 | 800 | 1000 | |
总计 | 1200 |
（1）根据图中的数据，试估计该款手机的平均使用时间；
（2）请将表格中的数据补充完整，并根据表中数据，判断是否有99．9％的把握认为“愿意购买该款手机”与“市民的年龄”有关．
参考公式：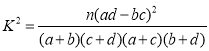
，其中
．
参考数据：
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
