题目内容
(本小题8分)
设函数 是定义域在
是定义域在 的函数,且
的函数,且 ,对于任意的实数
,对于任意的实数 ,都有
,都有 ,当
,当 >0时,
>0时, .
.
(1)求 的值;
的值;
(2)判断函数 在
在 的单调性并用定义证明;
的单调性并用定义证明;
(3)若 ,解不等式
,解不等式 .
.
【答案】
(1)  (2)
(2)  是
是 上是增函数. (3)
上是增函数. (3) 
【解析】解:(1)令 ,则
,则 ,
,
又因 ,所以
,所以 .
.
(2)任取 ,且
,且 ,则
,则 (其中
(其中 )
)





 ,由(1)知
,由(1)知 ,又
,又
 >0,
>0,



 是
是 上是增函数.
上是增函数.
证法二:作商法(略)
(3) 
 ,
,
 ,不等式即
,不等式即

 在
在 上是增函数,
上是增函数,

 ,得不等式的解集为
,得不等式的解集为

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
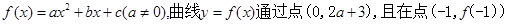
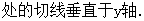
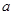 分别表示
分别表示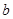 和
和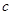 ;
;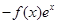 的单调区间。
的单调区间。