题目内容
知圆C:(x-1)2+y2=2,过点A(-1,0)的直线l将圆C分成弧长之比为1:3的两段圆弧,则直线l的方程为________.
 x-y+
x-y+ =0或
=0或 x+y+
x+y+ =0
=0分析:根据题意画出相应的图形,如图所示,连接CE,CF,过C作CD垂直于EF于点D,由圆C的方程找出圆心C的坐标和半径r,根据直线l将圆C分成弧长之比为1:3的两段圆弧,根据弧与圆心角的关系得到∠ECF为周角的
 ,求出∠ECF为直角,又CE=CF,可得出三角形ECF为等腰直角三角形,由CE及CF的长,利用勾股定理求出EF的长,再利用垂径定理得到D为EF中点,利用斜边上的中线等于斜边的一半求出CD的长,即为圆心距,设直线l的斜率为k,由A的坐标及k表示出直线l的方程,利用点到直线的距离公式表示出圆心C到直线l的距离d,让d等于CD的长列出关于k的方程,求出方程的解得到k的值,进而确定出直线l的方程.
,求出∠ECF为直角,又CE=CF,可得出三角形ECF为等腰直角三角形,由CE及CF的长,利用勾股定理求出EF的长,再利用垂径定理得到D为EF中点,利用斜边上的中线等于斜边的一半求出CD的长,即为圆心距,设直线l的斜率为k,由A的坐标及k表示出直线l的方程,利用点到直线的距离公式表示出圆心C到直线l的距离d,让d等于CD的长列出关于k的方程,求出方程的解得到k的值,进而确定出直线l的方程.解答:根据题意画出相应的图形,如图所示:

连接CE,CF,过C作CD⊥EF于点D,
由圆的方程(x-1)2+y2=2,得到圆心C(1,0),半径r=
 ,
,∵直线l将圆C分成弧长之比为1:3的两段圆弧,
∴∠ECF=
 ×360°=90°,又EC=FC=
×360°=90°,又EC=FC= ,
,∴△CEF为等腰直角三角形,
∴EF=
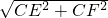 =2,
=2,∴CD=ED=FD=
 EF=1,
EF=1,设直线l的斜率为k,由A(-1,0),得到直线l方程为y=k(x+1),即kx-y+k=0,
∴圆心C到直线l的距离d=
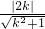 =1,即k2=
=1,即k2= ,
,解得:k=±
 ,
,则直线l的方程为
 x-y+
x-y+ =0或
=0或 x+y+
x+y+ =0.
=0.故答案为:
 x-y+
x-y+ =0或
=0或 x+y+
x+y+ =0
=0点评:此题考查了直线与圆相交的性质,涉及的知识有:圆的标准方程,垂径定理,等腰直角三角形的判定与性质,直线的点斜式方程,点到直线的距离公式,勾股定理,以及弦、弧、圆心角之间的关系,利用了数形结合的思想,是一道综合性较强的试题.

练习册系列答案
相关题目
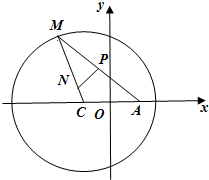 已知圆C:(x+1)2+y2=8.
已知圆C:(x+1)2+y2=8.