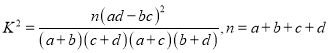题目内容
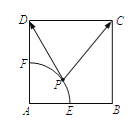
【题目】在正方体ABCD-A1B1C1D1的棱长为2，点P是上底面A1B1C1D1内一动点，则三棱锥P-ABC的三视图的面积之和最大值为（ ）
A.6B.7C.8D.9
【答案】C
【解析】
依题意可知三棱锥的主视图与左视图的面积的都为
，当
与
重合时三棱锥
的俯视图面积最大，从而求出三视图的面积和的最大值；
解：由题意可知，在主视图中的射影是在
上，
在主视图中，
在平面
上的射影是
，的射影到的距离是正方体的棱长；
左视图中，的射影是在
上，
在左视图中
在平面
三度射影是
，的射影到的距离是正方体的棱长，
所以三棱锥的主视图与左视图的面积的都为
；
当与重合时，三棱锥的俯视图为正方形
，
其面积最大，最大值为
，
故三棱锥P-ABC的三视图的面积之和最大值为
；
故选：C
练习册系列答案
相关题目
【题目】微信支付诞生于微信红包，早期知识作为社交的一部分“发红包”而诞生的，在发红包之余才发现，原来微信支付不仅可以用来发红包，还可以用来支付，现在微信支付被越来越多的人们所接受，现从某市市民中随机抽取300为对是否使用微信支付进行调查，得到下列
的列联表：
年轻人 | 非年轻人 | 总计 | |
经常使用微信支付 | 165 | 225 | |
不常使用微信支付 | |||
合计 | 90 | 300 |
根据表中数据，我们得到的统计学的结论是：由__________的把握认为“使用微信支付与年龄有关”。
|
|
|
|
|
|
|
|
|
|
|
|
其中
