题目内容
已知α的终边经过点(-4,3),求下列各式的值:
(1) ;
;
(2)sinα•cosα.
解:∵α的终边经过点P(-4,3),
∴|PO|=r=
因此, ,
, ,
, …(3分)
…(3分)
(1)根据诱导公式,得sin( ±α)=cosα,cos(π+α)=-cosα,sin(π-α)=sinα
±α)=cosα,cos(π+α)=-cosα,sin(π-α)=sinα
∴ …(5分)
…(5分)
(2)sinα•cosα=- ×
× =
=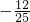 …(8分)
…(8分)
分析:(1)根据三角函数的定义,得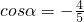 ,
,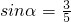 且
且 ,结合诱导公式化简,代入原式即可得所求的值;
,结合诱导公式化简,代入原式即可得所求的值;
(2)直接将sinα、cosα的值代入原式,即可得到sinα•cosα=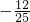 .
.
点评:本题根据三角函数的定义,求两个三角函数式的值,着重考查了任意角的三角函数、诱导公式和同角三角函数的关系等知识,属于基础题.
∴|PO|=r=

因此,
 ,
, ,
, …(3分)
…(3分)(1)根据诱导公式,得sin(
 ±α)=cosα,cos(π+α)=-cosα,sin(π-α)=sinα
±α)=cosα,cos(π+α)=-cosα,sin(π-α)=sinα∴
 …(5分)
…(5分)(2)sinα•cosα=-
 ×
× =
=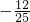 …(8分)
…(8分)分析:(1)根据三角函数的定义,得
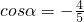 ,
,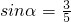 且
且 ,结合诱导公式化简,代入原式即可得所求的值;
,结合诱导公式化简,代入原式即可得所求的值;(2)直接将sinα、cosα的值代入原式,即可得到sinα•cosα=
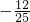 .
.点评:本题根据三角函数的定义,求两个三角函数式的值,着重考查了任意角的三角函数、诱导公式和同角三角函数的关系等知识,属于基础题.

练习册系列答案
相关题目
已知角α的终边经过点P(m,-3),且cosα=-
,则m等于( )
| 4 |
| 5 |
A、-
| ||
B、
| ||
| C、-4 | ||
| D、4 |