题目内容

已知不等式x2-3x+t＜0的解集为{x|1＜x＜m,x∈R},

(1)求t、m的值;

(2)若函数f(x)=-x2+ax+4在区间(-∞,1］上递增,求关于x的不等式loga(-mx2+3x+2-t)＜0的解集.

解：(1)由题意,1、m是方程x2-3x+t=0的两根,

    ∴

     (2)∵f(x)在(-∞,1)上递增,

    ∴≥1a≥2,而loga(-mx2+3x+2-t)=loga(-2x2+3x).

    故原不等式等价于0＜-2x2+3x＜1

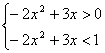
    *0＜x＜或1＜x＜.

    故原不等式的解集是{x|0＜x＜或1＜x＜}.

练习册系列答案
相关题目
已知不等式x2-3x+t＜0的解集为{x|1＜x＜m，x∈R}
（1）求t，m的值；
（2）若函数f（x）=-x2+ax+4在区间（-∞，1]上递增，求关于x的不等式loga（-mx2+3x+2-t）＜0的解集．
已知不等式x2-3x+m＜0的解集为{x|1＜x＜n，n∈R}，函数f（x）=-x2+ax+4．
（1）求m，n的值；
（2）若y=f（x）在（-∞，1]上递增，解关于x的不等式loga(-nx2+3x+2-m)＜0．

已知不等式x2–3x+t<0的解集为{x|1<x<m, m??R}

(1)求t, m的值；

(2)若f(x)= –x2+ax+4在(–∞,1)上递增，求不等式log a (–mx2+3x+2–t)<0的解集。
已知不等式x2-3x+t＜0的解集为{x|1＜x＜m，x∈R}
（1）求t，m的值；
（2）若函数f（x）=-x2+ax+4在区间（-∞，1]上递增，求关于x的不等式loga（-mx2+3x+2-t）＜0的解集．
已知不等式x2-3x+t＜0的解集为{x|1＜x＜m，x∈R}
（1）求t，m的值；
（2）若函数f（x）=-x2+ax+4在区间（-∞，1]上递增，求关于x的不等式loga（-mx2+3x+2-t）＜0的解集．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网