题目内容
7.设x,y满足约束条件$\left\{{\begin{array}{l}{x+y≤1}\\{x+1≥0}\\{x-y≤1}\end{array}}\right.$,则目标函数$z=\frac{y}{x-2}$的取值范围是$[{-\frac{2}{3},\frac{2}{3}}]$.分析 作出不等式组对应的平面区域,利用目标函数的几何意义,进行求解即可.
解答 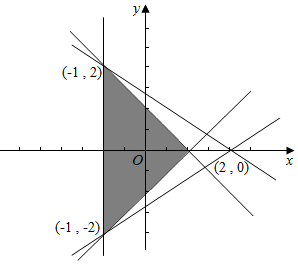 解:画出满足条件的平面区域,如图示:,
解:画出满足条件的平面区域,如图示:,
目标函数z=$\frac{y}{x-2}$几何意义为区域内的点与D(2,0)的斜率,
过(-1,2)与(2,0)时斜率最小,
过(-1,-2)与(2,0)时斜率最大,
∴Z最小值=$\frac{2}{-1-2}$=-$\frac{2}{3}$,Z最大值=$\frac{-2}{-1-2}$=$\frac{2}{3}$,
故答案为:$[{-\frac{2}{3},\frac{2}{3}}]$.
点评 本题主要考查线性规划和直线斜率的基本应用,利用目标函数的几何意义和数形结合是解决问题的基本方法.

练习册系列答案
相关题目
15.曲线(x+2y+a)(x2-y2)=0为平面上交于一点的三条直线的充要条件是( )
| A. | a=0 | B. | a=1 | C. | a=-1 | D. | a∈R |
2.曲线y=$\frac{1}{x}$(x>0)在点P(x0,y0)处的切线为l.若直线l与x,y轴的交点分别为A,B,则△OAB(其中O为坐标原点)的面积为( )
| A. | 4+2$\sqrt{2}$ | B. | 2$\sqrt{2}$ | C. | 2 | D. | 5+2$\sqrt{7}$ |
12.设集合A={a,a2,-2},B={2,4},A∩B={4},则a=( )
| A. | 2 | B. | -2 | C. | 4 | D. | $\sqrt{2}$ |
19.过双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左焦点F1作圆x2+y2=a2的切线,并延长交双曲线右支于点P,过右焦点F2作圆的切线交F1P于M,且M为F1P的中点,则双曲线的离心率e∈( )
| A. | (1,$\sqrt{2}$) | B. | ($\sqrt{2}$,$\sqrt{3}$) | C. | ($\sqrt{3},2$) | D. | (2,$\sqrt{5}$) |
16.设函数f(x)=-|x|,g(x)=lg(ax2-4x+1),若对任意x1∈R,都存在x2∈R,使f(x1)=g(x2),则实数a的取值范围为( )
| A. | (-∞,4] | B. | (0,4] | C. | (-4,0] | D. | [4,+∞) |
17.i是虚数单位,设复数z1=1+2i,z2=-3i,则z1•z1=( )
| A. | -6-3i | B. | 2-i | C. | 6-3i | D. | 6+3i |