题目内容

精英家教网如图，向量
OA
与x轴方向相同，向量
OB
与x轴正半轴的夹角为
2π
3
，|
OA
|=2，|
OB
|=1，且
OA
+
OB
+
OC
=
0
，则
OC
=
 
．
分析：先求出A、B两个点的坐标，根据
OA
+
OB
+
OC
=
0
，计算
OC
的坐标．
解答：解：由题意可知：A（2，0），即向量
OA
=（2，0）；
B(-
1
2
，-
3
2
)，则向量
OB
=(-
1
2
，-
3
2
)，
∵
OA
+
OB
+
OC
=
0
，∴
OC
=-(
OA
+
OB
)=(-
3
2
，
3
2
)
故答案为：(-
3
2
，
3
2
)
点评：本题考查平面向量数量积的运算，向量和复平面内的点的对应关系，是基础题．
练习册系列答案
相关题目
精英家教网（1）如图，向量
OA
和
OB
被矩阵M作用后分别变成
OA/
和
OB/
，
（Ⅰ）求矩阵M；（Ⅱ）并求y=sin(x+
π
3
)在M作用后的函数解析式；
（2）已知在直角坐标系x0y内，直线l的参数方程为
x=-2+tcos600
y=tsin600
(t为参数)．以Ox为极轴建立极坐标系，曲线C的极坐标方程为ρcos(θ-
π
3
)=
1
2
． 若C与L的交点为P，求点P与点A（-2，0）的距离|PA|
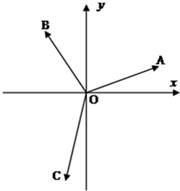如图，在平面直角坐标系xoy中，两个非零向量
OA
，
OB
与x轴正半轴的夹角分别为
π
6
和
2π
3
，向量
OC
满足
OA
+
OB
+
OC
=
0
，则
OC
与x轴正半轴夹角取值范围是（　　）
选修4-2：矩阵及其变换
（1）如图，向量
OA
和
OB
被矩阵M作用后分别变成
OA′
和
OB′
，
（Ⅰ）求矩阵M；
（Ⅱ）并求y=sin(x+
π
3
)在M作用后的函数解析式；
选修4-4：坐标系与参数方程
（ 2）在直角坐标系x0y中，直线l的参数方程为
x=3-
2
2
t
y=
5
+
2
2
t
（t为参数），在极坐标系（与直角坐标系x0y取相同的长度单位，且以原点O为极点，以x轴正半轴为极轴）中，圆C的方程为ρ=2
5
sinθ．
（Ⅰ）求圆C的直角坐标方程；
（Ⅱ）设圆C与直线l交于点A，B．若点P的坐标为（3，
5
），求|PA|+|PB|．
选修4-5：不等式选讲
（3）已知x，y，z为正实数，且
1
x
+
1
y
+
1
z
=1，求x+4y+9z的最小值及取得最小值时x，y，z的值．
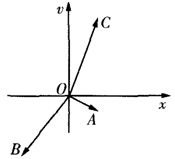精英家教网如图，非零向量
OA
，
OB
与x轴正半轴的夹角分别为
π
6
和
2π
3
，且
OA
+
OB
+
OC
=0，则
OC
与x轴正半轴的夹角的取值范围是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网