题目内容
圆经过点A（2，-3）和B（-2，-5）.（1）若圆的面积最小，求圆的方程；
（2）若圆心在直线x-2y-3=0上，求圆的方程.
（1）解：要使圆的面积最小，则AB为圆的直径，因为圆心是(0,-4),半径r=
,所以圆的方程为x2+(y+4)2=5.
（2）解法一：因为kAB=
,AB中点为（0，-4），得AB中垂线方程为y+4=-2x，即2x+y+4=0，解方程组
所以圆心为（-1，-2）.根据两点间的距离公式，得半径r=
,因此，所求的圆的方程为(x+1)2+(y+2)2=10.
解法二：所求圆的方程为(x-a)2+(y-b)2=r2，根据已知条件得
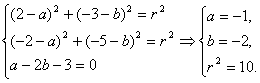
所以所求圆的方程为(x+1)2+(y+2)2=10.
练习册系列答案
相关题目
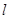：x-2y-3=0上，求此圆的标准方程.