题目内容
圆经过点A(2,-3)和B(-2,-5).
(1)若圆的面积最小,求圆的方程;
(2)若圆心在直线x-2y-3=0上,求圆的方程.
(1)若圆的面积最小,求圆的方程;
(2)若圆心在直线x-2y-3=0上,求圆的方程.
分析:(1)要使圆的面积最小,则AB为圆的直径,即求以AB为直径的圆.
(2)解法1,求出AB中垂线方程,与x-2y-3=0联立,求出圆心,再求出半径后即可得出圆的方程.
解法2,利用待定系数法,设为(x-a)2+(y-b)2=r2,求解.
(2)解法1,求出AB中垂线方程,与x-2y-3=0联立,求出圆心,再求出半径后即可得出圆的方程.
解法2,利用待定系数法,设为(x-a)2+(y-b)2=r2,求解.
解答:解:(1)要使圆的面积最小,则AB为圆的直径,所以所求圆的圆心为(0,-4),半径长
|AB|=
圆的方程为x2+(y+4)2=5
(2)解法1:因为kAB=12,AB中点为(0,-4),所以AB中垂线方程为y+4=-2x,即2x+y+4=0,解方程组
得
所以圆心为(-1,-2).根据两点间的距离公式,得半径r=
,因此,所求的圆的方程为(x+1)2+(y+2)2=10
解法2:所求圆的方程为(x-a)2+(y-b)2=r2,
根据已知条件得
⇒
所以所求圆的方程为(x+1)2+(y+2)2=10.
| 1 |
| 2 |
| 5 |
圆的方程为x2+(y+4)2=5
(2)解法1:因为kAB=12,AB中点为(0,-4),所以AB中垂线方程为y+4=-2x,即2x+y+4=0,解方程组
|
|
所以圆心为(-1,-2).根据两点间的距离公式,得半径r=
| 10 |
解法2:所求圆的方程为(x-a)2+(y-b)2=r2,
根据已知条件得
|
|
所以所求圆的方程为(x+1)2+(y+2)2=10.
点评:本题考查圆的方程求解,可以常用的方法有:定义法(即分别求出圆心、半径),待定系数法.若能充分利用圆的几何性质,可有效的减少计算量.问题(2)的两种解法能体现出这一点.

练习册系列答案
相关题目
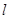 :x-2y-3=0上,求此圆的标准方程.
:x-2y-3=0上,求此圆的标准方程.