Question

已知圆经过点A（2，-3）和B（-2，-5），且圆心C在直线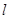：x-2y-3=0上，求此圆的标准方程.

 

Answer 1

【答案】

(x+1)²+(y+2)²=10

【解析】本试题主要考查了圆的标准方程的求解以及直线与圆的位置关系的运用。

解：圆经过A,B两点，所以圆心C在AB中垂线上

又AB中点坐标为（0，-4）,  k_AB=,

∴AB中垂线斜率等于-2

∴AB中垂线方程为：y+4=-2x即2x+y+4=0 ……………3分

又圆心C在直线：x-2y-3=0上

∴联立得   ……………………………6分

∴C(-1,-2)   …………………………………………………………9分

半径r=|AC|=

∴所求圆的方程为：(x+1)²+(y+2)²=10……………………………12分