题目内容
20.设数列{an}的前n项和为Sn,a1=10,an+1=9Sn+10.(Ⅰ)求证:{lgan}是等差数列;
(Ⅱ)设Tn是数列$\{\frac{3}{{(lg{a_n})(lg{a_{n+1}})}}\}$的前n项和,求Tn;
(Ⅲ)若${T_n}>\frac{1}{2}({m^2}-5m)$在n∈N*上有解,求整数m的取值集合.
分析 (1)an+1=9Sn+10,则当n≥2时,an=9Sn-1+10,相减化为an+1=10an,可得lgan+1-lgan=1,即可证明;
(II)由(I)可得:lgan=n.$\frac{3}{lg{a}_{n}lg{a}_{n+1}}$=$\frac{3}{n(n+1)}$=3$(\frac{1}{n}-\frac{1}{n+1})$.利用“裂项求和”即可得出.
(III)由${T_n}>\frac{1}{2}({m^2}-5m)$在n∈N*上有解,$\frac{1}{2}({m}^{2}-5m)$<(Tn)max,而Tn<3,可得$\frac{1}{2}({m}^{2}-5m)$<3,解出即可.
解答 (1)证明:∵an+1=9Sn+10,
∴当n≥2时,an=9Sn-1+10,可得an+1-an=9an,化为an+1=10an,
∴lgan+1-lgan=1,lga1=1.
∴{lgan}是等差数列,首项为1,公差为1.
(II)解:由(I)可得:lgan=1+(n-1)=n.
∴$\frac{3}{lg{a}_{n}lg{a}_{n+1}}$=$\frac{3}{n(n+1)}$=3$(\frac{1}{n}-\frac{1}{n+1})$.
∴Tn=$3[(1-\frac{1}{2})+(\frac{1}{2}-\frac{1}{3})$+…+$(\frac{1}{n}-\frac{1}{n+1})]$
=3$(1-\frac{1}{n+1})$=$\frac{3n}{n+1}$.
(III)∵${T_n}>\frac{1}{2}({m^2}-5m)$在n∈N*上有解,
∴$\frac{1}{2}({m}^{2}-5m)$<(Tn)max,
∵Tn<3,
∴$\frac{1}{2}({m}^{2}-5m)$<3,
解得-1<m<6,
∴整数m的取值集合为{0,1,2,3,4,5}.
点评 本题考查了递推关系的应用、等差数列的通项公式、“裂项求和”方法、对数的运算性质、不等式的性质,考查了转化能力、推理能力与计算能力,属于中档题.

| A. | a<b<c | B. | a<c<b | C. | b<a<c | D. | b<c<a |
| A. | 16π | B. | $2\sqrt{3}$ | C. | π | D. | 32π |
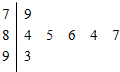 在广雅中学“十佳学生”评选的演讲比赛中,如图是七位评委为某学生打出的分数的茎叶图,去掉一个最高分和一个最低分后,所剩数据的众数和中位数分别为( )
在广雅中学“十佳学生”评选的演讲比赛中,如图是七位评委为某学生打出的分数的茎叶图,去掉一个最高分和一个最低分后,所剩数据的众数和中位数分别为( )| A. | 85,85 | B. | 84,86 | C. | 84,85 | D. | 85,86 |
| A. | 锐角三角形 | B. | 等腰三角形 | ||
| C. | 直角三角形 | D. | 等腰或直角三角形 |
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
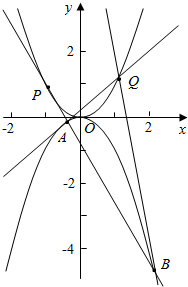 如图,过抛物线${C_1}:{x^2}=2py$上的一点Q与抛物线${C_2}:{x^2}=-2py$相切于A,B两点.若抛物线${C_1}:{x^2}=2py$的焦点F1到抛物线${C_2}:{x^2}=-2py$的焦点F2的距离为$\frac{1}{2}$
如图,过抛物线${C_1}:{x^2}=2py$上的一点Q与抛物线${C_2}:{x^2}=-2py$相切于A,B两点.若抛物线${C_1}:{x^2}=2py$的焦点F1到抛物线${C_2}:{x^2}=-2py$的焦点F2的距离为$\frac{1}{2}$