题目内容
已知 满足ax•f(x)=2bx+f(x),a≠0,f(1)=1且使f(x)=2x成立的实数x有且只有一个.
满足ax•f(x)=2bx+f(x),a≠0,f(1)=1且使f(x)=2x成立的实数x有且只有一个.(1)求f(x)的表达式;
(2)数列{an}满足:
 ,证明:{bn}为等比数列.
,证明:{bn}为等比数列.(3)在(2)的条件下,若
 ,求证:
,求证: .
.
【答案】分析:(1)由f(x)= ,知
,知 ,由此能求出f(x)的表达式.
,由此能求出f(x)的表达式.
(2)由bn+1=2bn,能够证明{bn}是首项为2,公比为2的等比数列.
(3)由bn=2n,知Cn= ,所以C2k+C2k+1=
,所以C2k+C2k+1= <
< .由此能够证明Sn<
.由此能够证明Sn< .
.
解答:解:(1)∵f(x)= ,
,
∴ ,
,
∴

(2)证明:∵ ,
,
∴ ,
,
bn+1=2bn,
∴{bn}是首项为2,公比为2的等比数列.
(3)∵bn=2n,
∴Cn=
∴C2k+C2k+1= <
<
∴n为奇数时,Sn=C1+(C2+C3)+…+(Cn-1+Cn)<1+
=1+ =
= <
<
n为偶数时,Sn<Sn+1<
综合以上,Sn<
点评:本题考查函数与数列的综合应用,解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化.
 ,知
,知 ,由此能求出f(x)的表达式.
,由此能求出f(x)的表达式.(2)由bn+1=2bn,能够证明{bn}是首项为2,公比为2的等比数列.
(3)由bn=2n,知Cn=
 ,所以C2k+C2k+1=
,所以C2k+C2k+1= <
< .由此能够证明Sn<
.由此能够证明Sn< .
.解答:解:(1)∵f(x)=
 ,
,∴
 ,
,∴


(2)证明:∵
 ,
,∴
 ,
,bn+1=2bn,
∴{bn}是首项为2,公比为2的等比数列.
(3)∵bn=2n,
∴Cn=

∴C2k+C2k+1=
 <
<
∴n为奇数时,Sn=C1+(C2+C3)+…+(Cn-1+Cn)<1+

=1+
 =
= <
<
n为偶数时,Sn<Sn+1<

综合以上,Sn<

点评:本题考查函数与数列的综合应用,解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 满足ax·f(x)=2bx+f(x), a≠0, f(1)=1且使
满足ax·f(x)=2bx+f(x), a≠0, f(1)=1且使 成立的实数x有且只有一个.
成立的实数x有且只有一个. 的表达式;
的表达式; 满足:
满足: , 证明:
, 证明: 为等比数列.
为等比数列. , 求证:
, 求证:
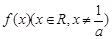 满足ax·f(x)=2bx+f(x), a≠0, f(1)=1且使
满足ax·f(x)=2bx+f(x), a≠0, f(1)=1且使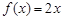 成立的实数x有且只有一个.
成立的实数x有且只有一个.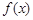 的表达式;
的表达式;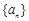 满足:
满足: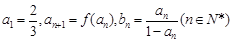 , 证明:
, 证明: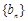 为等比数列.
为等比数列. , 求证:
, 求证: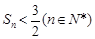
 满足ax•f(x)=2bx+f(x),a≠0,f(1)=1且使f(x)=2x成立的实数x有且只有一个.
满足ax•f(x)=2bx+f(x),a≠0,f(1)=1且使f(x)=2x成立的实数x有且只有一个. ,证明:{bn}为等比数列.
,证明:{bn}为等比数列. ,求证:
,求证: .
. 满足ax•f(x)=2bx+f(x),a≠0,f(1)=1且使f(x)=2x成立的实数x有且只有一个.
满足ax•f(x)=2bx+f(x),a≠0,f(1)=1且使f(x)=2x成立的实数x有且只有一个. ,证明:{bn}为等比数列.
,证明:{bn}为等比数列. ,求证:
,求证: .
.