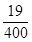题目内容
设甲、乙两人每次射击命中目标的概率分别是
和
,且各次射击相互独立.
(1)若甲、乙各射击1次,求至少有一人命中目标的概率;
(2)若甲、乙各射击2次,求两人命中目标的次数相等的概率.
| 2 |
| 3 |
| 4 |
| 5 |
(1)若甲、乙各射击1次,求至少有一人命中目标的概率;
(2)若甲、乙各射击2次,求两人命中目标的次数相等的概率.
分析:(1)先求出两个人都没有击中目标的概率,再用1减去此概率,即得所求.
(2)先求出两个人都没有击中目标的概率、两个人都击中一次的概率、两个人都击中2次的概率,相加,即得所求.
(2)先求出两个人都没有击中目标的概率、两个人都击中一次的概率、两个人都击中2次的概率,相加,即得所求.
解答:解:(1)若甲、乙各射击1次,两个人都没有击中目标的概率为
×
=
,
故至少有一人命中目标的概率为1-
=
.
(2)若甲、乙各射击2次,则两个人都没有击中目标的概率为
×
=
,
两个人都击中一次的概率为
×
×
×
×
×
=
,
两个人都击中2次的概率为 (
)2•(
)2=
,
故两人命中目标的次数相等的概率为
+
+
=
.
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 15 |
故至少有一人命中目标的概率为1-
| 1 |
| 15 |
| 14 |
| 15 |
(2)若甲、乙各射击2次,则两个人都没有击中目标的概率为
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 15 |
两个人都击中一次的概率为
| C | 1 2 |
| 2 |
| 3 |
| 1 |
| 3 |
| C | 1 2 |
| 4 |
| 5 |
| 1 |
| 5 |
| 32 |
| 225 |
两个人都击中2次的概率为 (
| 2 |
| 3 |
| 4 |
| 5 |
| 64 |
| 225 |
故两人命中目标的次数相等的概率为
| 1 |
| 15 |
| 32 |
| 225 |
| 64 |
| 225 |
| 111 |
| 225 |
点评:本题主要考查相互独立事件的概率乘法公式,所求的事件与它的对立事件概率间的关系,属于中档题.

练习册系列答案
相关题目
 和
和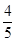 ,且各次射击相互独立,若按甲、乙、甲、乙、…的次序轮流射击,直到有一人击中目标就停止射击,则射击停止时,甲射击了两次的概率是
( )
,且各次射击相互独立,若按甲、乙、甲、乙、…的次序轮流射击,直到有一人击中目标就停止射击,则射击停止时,甲射击了两次的概率是
( )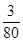 B、
B、 C、
C、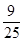 D、
D、