题目内容
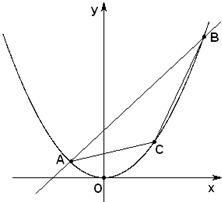 已知直线y=2x+1与抛物线x2=4y交于A,B两点,O为坐标原点.点C位于抛物线弧AOB上,求点C坐标使得△ABC面积最大.
已知直线y=2x+1与抛物线x2=4y交于A,B两点,O为坐标原点.点C位于抛物线弧AOB上,求点C坐标使得△ABC面积最大.分析:直线为y=2x+1,要使得内接△ABC面积最大,则只须使得过C(xc,yc)点的切线与直线y=2x+1平行,由导数的性质能求出C位于(4,4)点处时,△ABC面积最大.
解答:解:∵直线为y=2x+1,
∴要使得内接△ABC面积最大,则只须使得过C(xc,yc)点的切线与直线y=2x+1平行,
∵x2=4y,
∴y=
,
∵y′=
×2x,直线y=2x+1的斜率为2,
∴过C(xc,yc)点的切线斜率k=yc′=
×2xc=2,
解得xc=4,则可得yc=4
∴C位于(4,4)点处时,△ABC面积最大.
∴要使得内接△ABC面积最大,则只须使得过C(xc,yc)点的切线与直线y=2x+1平行,
∵x2=4y,
∴y=
| x2 |
| 4 |
∵y′=
| 1 |
| 4 |
∴过C(xc,yc)点的切线斜率k=yc′=
| 1 |
| 4 |
解得xc=4,则可得yc=4
∴C位于(4,4)点处时,△ABC面积最大.
点评:本题主要考查抛物线标准方程,简单几何性质,直线与抛物线的位置关系等基础知识.考查运算求解能力,推理论证能力;考查化归与转化思想.解题时要认真审题,注意导数性质的灵活运用.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目

