题目内容
已知直线y=2x-1与曲线y=ln(x+a)相切,则a的值为
ln2
ln2.
| 1 |
| 2 |
| 1 |
| 2 |
分析:设出切点P(m,ln(m+a)),根据导数的几何意义,且切点在切线上,列出关于m和a的方程组,求解方程组,即可得到a的值.
解答:解:设切点坐标为P(m,ln(m+a)),
∵曲线y=ln(x+a),
∴y′=
,
∵直线y=2x-1与曲线y=ln(x+a)相切,
∴y′|x=m=
=2,①
又切点P(m,ln(m+a))在切线y=2x-1上,
∴ln(m+a)=2m-1,②
由①②可得,a=
ln2,
∴a的值为
ln2.
故答案为:
ln2.
∵曲线y=ln(x+a),
∴y′=
| 1 |
| x+a |
∵直线y=2x-1与曲线y=ln(x+a)相切,
∴y′|x=m=
| 1 |
| m+a |
又切点P(m,ln(m+a))在切线y=2x-1上,
∴ln(m+a)=2m-1,②
由①②可得,a=
| 1 |
| 2 |
∴a的值为
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:本题考查了利用导数研究曲线上某点切线方程.导数的几何意义即在某点处的导数即该点处切线的斜率,解题时要注意运用切点在曲线上和切点在切线上.属于中档题.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
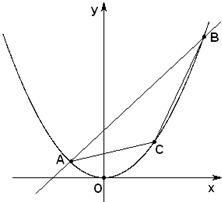 已知直线y=2x+1与抛物线x2=4y交于A,B两点,O为坐标原点.点C位于抛物线弧AOB上,求点C坐标使得△ABC面积最大.
已知直线y=2x+1与抛物线x2=4y交于A,B两点,O为坐标原点.点C位于抛物线弧AOB上,求点C坐标使得△ABC面积最大.
