题目内容
已知直线y=2x+1与抛物线x2=4y交于A,B两点,O为坐标原点.点C位于抛物线弧AOB上,求点C坐标使得△ABC面积最大.

解:∵直线为y=2x+1,
∴要使得内接△ABC面积最大,则只须使得过C(xc,yc)点的切线与直线y=2x+1平行,
∵x2=4y,
∴ ,
,
∵ ,
,
直线y=2x+1的斜率为2,
∴过C(xc,yc)点的切线斜率k=yc'= ,
,
解得xc=4,则可得yc=4
∴C位于(4,4)点处时,△ABC面积最大.
∴要使得内接△ABC面积最大,则只须使得过C(xc,yc)点的切线与直线y=2x+1平行,
∵x2=4y,
∴
 ,
,∵
 ,
,直线y=2x+1的斜率为2,
∴过C(xc,yc)点的切线斜率k=yc'=
 ,
,解得xc=4,则可得yc=4
∴C位于(4,4)点处时,△ABC面积最大.

练习册系列答案
相关题目
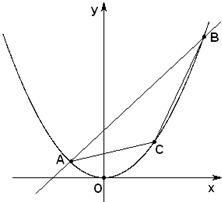 已知直线y=2x+1与抛物线x2=4y交于A,B两点,O为坐标原点.点C位于抛物线弧AOB上,求点C坐标使得△ABC面积最大.
已知直线y=2x+1与抛物线x2=4y交于A,B两点,O为坐标原点.点C位于抛物线弧AOB上,求点C坐标使得△ABC面积最大.