题目内容
已知正方形![]() 的中心在原点,四个顶点都在函数
的中心在原点,四个顶点都在函数![]() 图象上.
图象上.
(1)若正方形的一个顶点为![]() ,求
,求![]() ,
,![]() 的值,并求出此时函数的单调增区间;
的值,并求出此时函数的单调增区间;
(2)若正方形![]() 唯一确定,试求出
唯一确定,试求出![]() 的值.www..com
的值.www..com
(1)因为一个顶点为![]() ,所以必有另三个顶点
,所以必有另三个顶点![]() ,
,![]() ,
,![]() ,
,
将![]() ,
,![]() 代入
代入![]() ,得
,得![]() ,
,![]() . …………………4分
. …………………4分
所以![]() .
.
因为![]() ,令
,令![]() ,得
,得![]() 或
或![]() ,
,
所以函数![]() 单调增区间为
单调增区间为![]() 和
和![]() .……………………6分
.……………………6分
(2)设正方形![]() 对角线
对角线![]() 所在的直线方程为
所在的直线方程为![]() ,则对角线
,则对角线![]() 所在的直线方程为
所在的直线方程为![]() .
.
由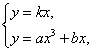 解得
解得![]() ,
,
所以![]() ,
,
同理,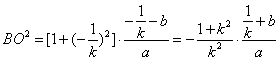 ,
,
又因为![]() ,所以
,所以![]() .……………………………10分
.……………………………10分
即![]() ,即
,即![]() .
.
令![]() 得
得![]()
因为正方形![]() 唯一确定,则对角线
唯一确定,则对角线![]() 与
与![]() 唯一确定,于是
唯一确定,于是![]() 值唯一确定,
值唯一确定,
所以关于![]() 的方程
的方程![]() 有且只有一个实数根,又
有且只有一个实数根,又![]() .
.
所以![]() ,即
,即![]() .………………………………………14分
.………………………………………14分
因为![]() ,
,![]() ,所以
,所以![]() ;又
;又 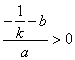 ,所以
,所以![]() ,故
,故![]() .
.
因此![]() ;
;
反过来![]() 时,
时,![]() ,
,![]() ,
,
于是![]() ,
,![]() ;或
;或![]() ,
,![]()
于是正方形![]() 唯一确定.……………………………………………………16分
唯一确定.……………………………………………………16分

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
 的中心在原点,四个顶点都在函数
的中心在原点,四个顶点都在函数 图象上,且正方形的一个顶点为
图象上,且正方形的一个顶点为 .
. ,
, 的值;
的值; +1,
+1, 的中心在原点,四个顶点都在函数
的中心在原点,四个顶点都在函数 图象上,且正方形的一个顶点为
图象上,且正方形的一个顶点为 .
. ,
, 的值;
的值;