题目内容
已知正方形![]() 的中心在原点,四个顶点都在函数
的中心在原点,四个顶点都在函数![]() 图象上.
图象上.
(1)若正方形的一个顶点为![]() ,求
,求![]() ,
,![]() 的值,并求出此时函数的单调增区间;
的值,并求出此时函数的单调增区间;
(2)若正方形![]() 唯一确定,试求出
唯一确定,试求出![]() 的值.
的值.
⑴因为![]() ,所以
,所以![]() ,因此
,因此![]() ,
,
所以函数![]() 的图象在点
的图象在点![]() 处的切线方程为
处的切线方程为![]() ,…………………………2分
,…………………………2分
由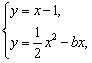 得
得![]() ,由
,由![]() ,得
,得![]() .…4分
.…4分
⑵因为![]() ,
,
所以![]() ,由题意知
,由题意知![]() 在
在![]() 上有解,
上有解,
因为![]() ,设
,设![]() ,因为
,因为![]() ,
,
则只要 解得
解得![]() ,
,
所以b的取值范围![]() .………………………………………………………………8分
.………………………………………………………………8分
⑶不妨设![]() .因为函数
.因为函数![]() 在区间
在区间![]() 上是增函数,所以
上是增函数,所以![]() ,
,
函数![]() 图象的对称轴为
图象的对称轴为![]() ,且
,且![]() ,
,
(ⅰ)当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上是减函数,所以
上是减函数,所以![]() ,
,
所以![]() 等价于
等价于![]() ,
,
即![]() ,
,
等价于![]() 在区间
在区间![]() 上是增函数,
上是增函数,
等价于![]() 在区间
在区间![]() 上恒成立,
上恒成立,
等价于![]() 在区间
在区间![]() 上恒成立,
上恒成立,
所以![]() ,又
,又![]() ,
,
所以![]() ;………………………………………………………………………………………10分
;………………………………………………………………………………………10分
(ⅱ)当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上是减函数,在
上是减函数,在![]() 上为增函数.
上为增函数.
①当![]() 时,
时,
![]() 等价于
等价于![]() ,
,
等价于![]() 在区间
在区间![]() 上是增函数,
上是增函数,
等价于![]() 在区间
在区间![]() 上恒成立,
上恒成立,
等价于![]() 在区间
在区间![]() 上恒成立,
上恒成立,
所以![]() ,又
,又![]() ,
,
所以![]() ;……………………………………………………………………………12分
;……………………………………………………………………………12分
②当![]() 时,
时,
![]() 等价于
等价于![]() ,
,
等价于![]() 在区间
在区间![]() 上是增函数,
上是增函数,
等价于![]() 在区间
在区间![]() 上恒成立,
上恒成立,
等价于![]() 在区间
在区间![]() 上恒成立,
上恒成立,
所以![]() ,故
,故![]() .………………………………………………………………14分
.………………………………………………………………14分
③当![]() 时,
时,
由![]() 图象的对称性知,只要
图象的对称性知,只要![]() 对于①②同时成立,那么对于③,
对于①②同时成立,那么对于③,
则存在![]() ,
,
使![]() 恒成立;
恒成立;
或存在![]() ,
,
使![]() 恒成立.
恒成立.
因此,![]() .
.
综上,b的取值范围是![]() .……………………………………………………16分
.……………………………………………………16分

练习册系列答案
相关题目
 的中心在原点,四个顶点都在函数
的中心在原点,四个顶点都在函数 图象上,且正方形的一个顶点为
图象上,且正方形的一个顶点为 .
. ,
, 的值;
的值; +1,
+1, 的中心在原点,四个顶点都在函数
的中心在原点,四个顶点都在函数 图象上,且正方形的一个顶点为
图象上,且正方形的一个顶点为 .
. ,
, 的值;
的值;