题目内容
(本小题14分)已知函数f(x)= ,x∈[1,+∞
,x∈[1,+∞
(1)当a= 时,求函数f(x)的最小值
时,求函数f(x)的最小值
(2)若对任意x∈[1,+∞ ,f(x)>0恒成立,试求实数a的取值范围
,f(x)>0恒成立,试求实数a的取值范围
(3)求f(x)的最小值
【答案】
解(1) 当a= 时,f(x)=x+
时,f(x)=x+ +2
+2
∵f(x)在区间[1,+∞ 上为增函数,
上为增函数,
∴f(x)在区间[1,+∞ 上的最小值为f(1)=
上的最小值为f(1)= .。。。。。。。。。。4
.。。。。。。。。。。4
(2)在区间[1,+∞ 上,f(x)=
上,f(x)=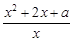 >0恒成立
>0恒成立 x2+2x+a>0恒成立
x2+2x+a>0恒成立
即
 a> x2+2x(x
a> x2+2x(x )恒成立,∵函数y= x2+2x(x
)恒成立,∵函数y= x2+2x(x )的最大值为-3
)的最大值为-3
∴a>-3.。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。8
(3) f(x)=x+ +2,x∈[1,+∞
+2,x∈[1,+∞
当a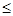 0时,函数f(x)递增,故当x=1时,f (x)min=3+a,
0时,函数f(x)递增,故当x=1时,f (x)min=3+a,
 当0<a<1时,函数f(x)递增,故当x=1时,f(x)min=3+a,
当0<a<1时,函数f(x)递增,故当x=1时,f(x)min=3+a,
当a 时 f(x)=x+
时 f(x)=x+ +2
+2 +2(当且仅当x=
+2(当且仅当x= 时取“=”)
时取“=”)
f(x)min= +2.。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。14
+2.。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。14
【解析】略

练习册系列答案
相关题目
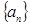 满足
满足 ,且
,且 是
是 ,
, 的等差中项.
的等差中项. ,
, ,求使
,求使  成立的正整数
成立的正整数 的最小值.
的最小值. ,设
,设 。
。 图象上任意一点
图象上任意一点 为切点的切线的斜率
为切点的切线的斜率 恒成立,求实数
恒成立,求实数 的最小值。
的最小值。 ,使得函数
,使得函数 的图象与
的图象与 的图象恰好有四个不同的交点?若存在,求出
的图象恰好有四个不同的交点?若存在,求出 的图像与函数
的图像与函数 的图像关于点
的图像关于点 对称
对称 ,
, 在区间
在区间 上的值不小于6,求实数a的取值范围.
上的值不小于6,求实数a的取值范围. 的图像在[a,b]上连续不断,定义:
的图像在[a,b]上连续不断,定义: ,
, ,其中
,其中 表示函数
表示函数 在D上的最小值,
在D上的最小值, 表示函数
表示函数 对任意的
对任意的 成立,则称函数
成立,则称函数 上的“k阶收缩函数”
上的“k阶收缩函数” ,试写出
,试写出 ,
, 的表达式;
的表达式; 试判断
试判断 ,函数
,函数 是[0,b]上的2阶收缩函数,求b的取值范围
是[0,b]上的2阶收缩函数,求b的取值范围