题目内容
(本小题14分)
已知等比数列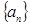 满足
满足 ,且
,且 是
是 ,
, 的等差中项.
的等差中项.
(Ⅰ)求数列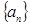 的通项公式;
的通项公式;
(Ⅱ)若 ,
, ,求使
,求使  成立的正整数
成立的正整数 的最小值.
的最小值.
【答案】
(1) (2)使
(2)使 成立的正整数
成立的正整数 的最小值为10
的最小值为10
【解析】
试题分析:解:(Ⅰ)设等比数列 的首项为
的首项为 ,公比为
,公比为 ,
,
依题意,有 即
即
由  得
得  ,解得
,解得 或
或 .
.
当 时,不合题意舍;
时,不合题意舍;
当 时,代入(2)得
时,代入(2)得 ,所以,
,所以, .
.
(Ⅱ)
 .
.
所以


因为 ,所以
,所以 ,
,
即 ,解得
,解得 或
或 .
.
因为 ,故使
,故使 成立的正整数
成立的正整数 的最小值为10 .
的最小值为10 .
考点:等差数列和等比数列
点评:解决该试题的关键是对于等差数列和等比数列的通项公式和性质的熟练运用,以及分组求和,属于基础题。

练习册系列答案
相关题目
 .
. ,点P为曲线
,点P为曲线 上的一个动点,求以点P为切点的切线斜率取最小值时的切线方程;
上的一个动点,求以点P为切点的切线斜率取最小值时的切线方程; 上为单调增函数,试求
上为单调增函数,试求 的取值范围.
的取值范围. 满足:
满足: ,
, ,且该函数的最小值为1.
,且该函数的最小值为1. =
=  .(其中
.(其中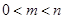 ). 问是否存在这样的两个实数
). 问是否存在这样的两个实数 ,使得函数
,使得函数
 且函数
且函数 在区间
在区间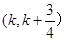 上存在极值,求实数
上存在极值,求实数 的取值范围;
的取值范围; 时,不等式
时,不等式 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围; ,
, ……
…… .
. ,x∈[1,+∞
,x∈[1,+∞
 时,求函数f(x)的最小值
时,求函数f(x)的最小值 
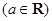 .
. ,求曲线
,求曲线 在
在 处切线的斜率;
处切线的斜率; 的单调区间;
的单调区间; ,若对任意
,若对任意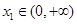 ,均存在
,均存在 ,使得
,使得 ,求
,求 的取值范围。
的取值范围。