题目内容
已知![]() ,
,![]() ,
,![]() .
.
(1)当![]() 时,试比较
时,试比较![]() 与
与![]() 的大小关系;
的大小关系;
(2)猜想![]() 与
与![]() 的大小关系,并给出证明.
的大小关系,并给出证明.
![]() 时,
时,![]() ,
,![]() 时,
时,![]() ,
,![]() 时,
时,![]() ,
,
所以猜想:![]() 时,
时,![]() .…………………………………………………3分
.…………………………………………………3分
证明:不等式即为![]() .
.
⑴当![]() 时,左边
时,左边![]() ,右边
,右边![]() ,
,![]() 成立,
成立,
⑵假设当![]() 时,原不等式成立,即
时,原不等式成立,即![]() ,
,
则当![]() 时,左边
时,左边![]() ,右边
,右边![]() ,
,
要证![]() 成立, 即证
成立, 即证![]() ,即证
,即证![]() ,
,
事实上,由二项式定理,得
![]() ,
,
即当![]() 时,原不等式也成立.
时,原不等式也成立.
由⑴⑵可得当![]() 时,不等式
时,不等式![]() 成立.……………………………10分
成立.……………………………10分

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知符号函数sgn x=
则方程x+1=(2x-1)sgnx的所有解之和是( )
|
| A、0 | ||||
| B、2 | ||||
C、-
| ||||
D、
|
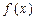 ,如果满足:对任意
,如果满足:对任意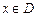 ,存在常数
,存在常数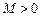 ,都有
,都有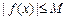 成立,则称
成立,则称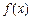 是D上的有界函数,其中M称为函数
是D上的有界函数,其中M称为函数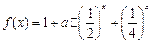 ;
;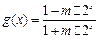 .
. 上的值域,并判断函数
上的值域,并判断函数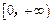 上是以3为上界的
上是以3为上界的 有界函数,求实数a的取值范围;
有界函数,求实数a的取值范围;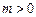 ,函
,函 数
数 在
在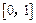 上的上界是
上的上界是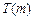 ,求
,求 ,如果满足:对任意
,如果满足:对任意 ,存在常数
,存在常数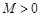 ,都有
,都有 成立,则称
成立,则称 是D上的有界函数,其中M称为函数
是D上的有界函数,其中M称为函数 ;
; .
. 上的值域,并判断函数
上的值域,并判断函数 上是以3为上界的有界函数,求实数a的取值范围;
上是以3为上界的有界函数,求实数a的取值范围; ,函数
,函数 在
在 上的上界是
上的上界是 ,求
,求