题目内容
【题目】设函数![]() ,
,![]() .
.
(Ⅰ)讨论函数![]() 的单调性;
的单调性;
(Ⅱ)当![]() 时,函数
时,函数![]() 恰有两个零点
恰有两个零点![]() ,证明:
,证明:![]()
【答案】(1) 当![]() 时,
时,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增;当
上单调递增;当![]() 时,
时,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
(2)证明见解析.
【解析】分析:(1)对函数![]() 求导,令
求导,令![]() ,
,![]() ,分
,分![]() ,判断出单调性;(2)采用综合分析法证明, 由已知条件求出
,判断出单调性;(2)采用综合分析法证明, 由已知条件求出 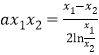 ,要证明
,要证明![]() ,即证
,即证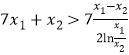 ,即证
,即证 ,令
,令![]() ,通过证明
,通过证明![]() ,得出结论。
,得出结论。
详解: (Ⅰ)![]() .
.
∵![]() ,∴由
,∴由![]() ,得
,得![]() ,即
,即![]() .
.
若![]() ,当
,当![]() 变化时,
变化时,![]() ,
,![]() 的变化情况如下表
的变化情况如下表
|
|
|
|
| 单调递减 | 极小值 | 单调递增 |
若![]() ,当
,当![]() 变化时,
变化时,![]() ,
,![]() 的变化情况如下表:
的变化情况如下表:
|
|
|
|
| + | 0 | - |
| 单调递增 | 极大值 | 单调递减 |
综上,当![]() 时,
时,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增;
上单调递增;
当![]() 时,
时,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
(Ⅱ)∵当![]() 时,函数
时,函数![]() 恰有两个零点
恰有两个零点![]() ,
,![]()
![]() ,
,
则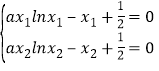 ,即
,即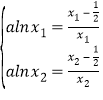 .
.
两式相减,得![]()
∵![]() ,∴
,∴![]() ,∴
,∴![]() ,∴
,∴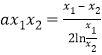 .
.
∴要证![]() ,即证
,即证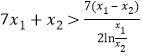 ,即证
,即证![]()
即证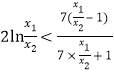
令![]()
![]() ,则即证
,则即证![]() .
.
设![]() ,即证
,即证![]() 在
在![]() 恒成立.
恒成立.
![]() .
.
∵![]() 在
在![]() 恒成立.∴
恒成立.∴![]() 在
在![]() 单调递增.
单调递增.
∵![]() 在
在![]() 是连续函数,
是连续函数,
∴当![]() 时,
时,![]()
∴当![]() 时,有
时,有![]() .
.

练习册系列答案
相关题目