题目内容
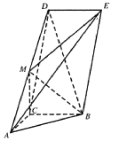
【题目】如图，在多面体
中，已知四边形
为平行四边形，平面
平面
，
为
的中点，
，
，
，
.
(Ⅰ)求证：
平面；
(Ⅱ)求二面角
的余弦值
【答案】(1)证明见解析.
(2) 
.
【解析】分析：（1）通过面面垂直的性质定理得出线面垂直；（2）以点
为坐标原点，
所在直线分别为
轴，
轴，
轴建立如图所示的空间直角坐标系
，写出每个点的坐标，分别求出平面DBM,BME的一个法向量，由向量夹角公式，求出二面角的平面角的余弦值即可。
详解： (Ⅰ)在
中，∵
，
，
，∴
∴由勾股定理的逆定理，得
又
，
，∴
平面
∵
平面，∴
∵平面
平面
，且平面
平面
，平面
∴
平面
(Ⅱ)∵平面，∴
.
又，，
故以点为坐标原点，所在直线分别为轴，轴，轴建立如图所示的空间直角坐标系
∴
，
，
，
，
∴
，
，
设平面
的法向量为
.
由
，得
.取
，∴
.
设平面
的法向量为
.
由
，得
.取
，∴
∴
∵二面角
为锐二面角，故其余弦值为.
【题目】某同学用“五点法”画函数
在某一个周期内的图象时，列表并填入了部分数据，如下表：
|
|
|
|
|
|
|
|
| |||
|
|
|
|
|
（1）请将上表数据补充完整；函数
的解析式为
（直接写出结果即可）；
（2）根据表格中的数据作出一个周期的图象；
（3）求函数在区间
上的最大值和最小值．
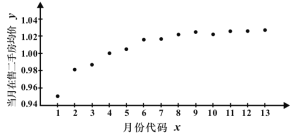
【题目】如图是某小区2017年1月至2018年1月当月在售二手房均价（单位：万元/平方米）的散点图.（图中月份代码1—13分别对应2017年1月—2018年1月）
由散点图选择
和
两个模型进行拟合，经过数据处理得到两个回归方程分别为
和
，并得到以下一些统计量的值：
|
| |
残差平方和 | 0.000591 | 0.000164 |
总偏差平方和 | 0.006050 | |
（1）请利用相关指数
判断哪个模型的拟合效果更好；
（2）某位购房者拟于2018年6月份购买这个小区
平方米的二手房（欲
购房为其家庭首套房）.若购房时该小区所有住房的房产证均已满2年但未满5年，请你利用（1）中拟合效果更好的模型估算该购房者应支付的购房金额.（购房金额=房款+税费；房屋均价精确到0.001万元/平方米）
附注：根据有关规定，二手房交易需要缴纳若干项税费，税费是按房屋的计税价格进行征收.（计税价格=房款），征收方式见下表：
契税 （买方缴纳） | 首套面积90平方米以内（含90平方米）为1%；首套面积90平方米以上且144平方米以内（含144平方米）为1.5%；面积144平方米以上或非首套为3% |
增值税 （卖方缴纳） | 房产证未满2年或满2年且面积在144平方米以上（不含144平方米）为5.6%；其他情况免征 |
个人所得税 （卖方缴纳） | 首套面积144平方米以内（含144平方米）为1%；面积144平方米以上或非首套均为1.5%；房产证满5年且是家庭唯一住房的免征 |
参考数据：
，
，
，
，
，
，
，
. 参考公式：相关指数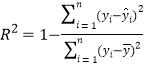
.