题目内容
已知数列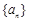 的前
的前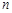 项和为
项和为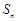 满足
满足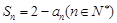 .
.
(1)函数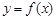 与函数
与函数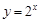 互为反函数,令
互为反函数,令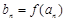 ,求数列
,求数列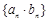 的前
的前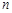 项和
项和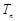 ;
;
(2)已知数列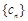 满足
满足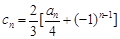 ,证明:对任意的整数
,证明:对任意的整数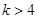 ,有
,有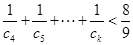 .
.
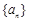 的前
的前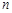 项和为
项和为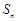 满足
满足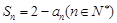 .
.(1)函数
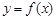 与函数
与函数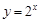 互为反函数,令
互为反函数,令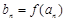 ,求数列
,求数列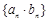 的前
的前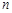 项和
项和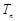 ;
;(2)已知数列
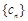 满足
满足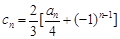 ,证明:对任意的整数
,证明:对任意的整数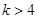 ,有
,有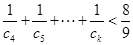 .
.(1) ; (2)见解析
; (2)见解析
 ; (2)见解析
; (2)见解析试题分析:(1)先由题意求出
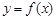 的解析式,再利用数列前n项和与第n项关系,求出
的解析式,再利用数列前n项和与第n项关系,求出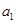 及第n项与第n-1项的递推关系,结合等比数列的定义知数列
及第n项与第n-1项的递推关系,结合等比数列的定义知数列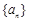 是等比数列,再根据等比数列通项公式求出
是等比数列,再根据等比数列通项公式求出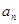 的通项公式,由对数函数与指数函数互为反函数结合已知条件求出
的通项公式,由对数函数与指数函数互为反函数结合已知条件求出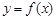 的解析式,将
的解析式,将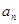 的通项公式代入
的通项公式代入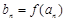 求出
求出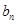 的通项公式,利用数列求和方法求出
的通项公式,利用数列求和方法求出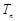 ;(2)求出
;(2)求出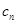 的通项公式,将不等式左边具体化,利用放缩法化成等比数列求和问题求出和,通过放缩所证不等式.
的通项公式,将不等式左边具体化,利用放缩法化成等比数列求和问题求出和,通过放缩所证不等式.试题解析:(1)由
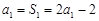 ,得
,得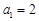
当
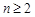 时,有
时,有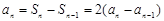 ,
,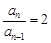
所以数列
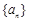 是以2为首项,2为公比的等比数列,所以
是以2为首项,2为公比的等比数列,所以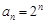
由题意得
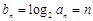 ,所以
,所以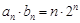
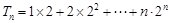 ①
①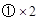 得
得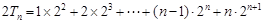 ②
②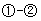 得
得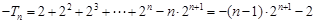 ,所以
,所以
(2)由通项公式得
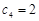 ,当
,当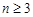 且
且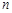 为奇数时
为奇数时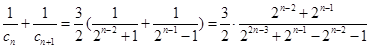
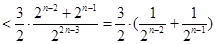
当
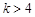 且
且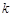 为偶数时
为偶数时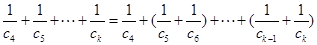
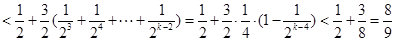
当
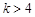 且
且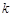 为奇数时
为奇数时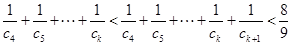
所以对任意的整数
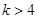 ,有
,有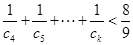 .
.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
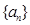 中抽出一些项,依原来的顺序组成的新数列叫数列
中抽出一些项,依原来的顺序组成的新数列叫数列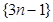 的一个是等比数列的子列;
的一个是等比数列的子列;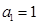 ,公比
,公比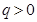 且
且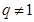 ,则数列
,则数列 是公差不等于0的等差数列,
是公差不等于0的等差数列,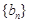 是等比数列
是等比数列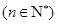 ,且
,且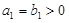 .
.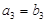 ,比较
,比较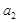 与
与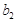 的大小关系;
的大小关系;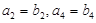 .(ⅰ)判断
.(ⅰ)判断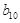 是否为数列
是否为数列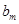 是数列
是数列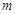 的集合(不必说明理由).
的集合(不必说明理由).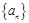 的前
的前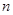 项和为
项和为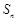 ,首项
,首项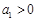 ,
,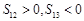 .则以下关于数列
.则以下关于数列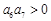 ;②
;②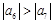 ;③
;③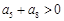 ;④前
;④前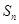 中最大的项为第六项
中最大的项为第六项 的前
的前 项和为
项和为 ,若
,若 ,则
,则



 中,若公差
中,若公差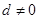 ,且
,且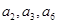 成等比数列,则公比
成等比数列,则公比 .
.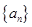 的前
的前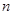 项和为
项和为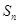 ,且4
,且4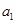 ,2
,2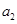 ,
,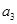 成等差数列。若
成等差数列。若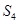 =( )
=( ) 的前项和为
的前项和为 ,若
,若 ,
, ,则
,则 等于 .
等于 .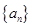 中,
中,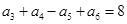 ,则
,则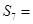 ( )
( )