题目内容
在△ABC中,余弦定理可叙述为a2=b2+c2-2bccosA.?其中a、b、c依次为角A、B、C的对边,类比以上定理,给出空间四面体性质的猜想.?
解:如例4图示,S1、S2、S3、S分别表示△PAB、△PBC、△PCA、△ABC的面积,α、β、γ依次表示平面PAB与平面PBC,平面PBC与平面PCA,平面PCA与平面PAB所成二面角的大小,猜想余弦定理类比推理到三维空间的表现形式应为?
S2=S12+S22+S32-2S1S2cosα-2S2S3cosβ-2S3S1cosγ.?
上式可叙述为四面体的一个面的面积的平方,等于其他各面面积平方的和,减去每两个面面积与这两个面夹角余弦乘积的两倍.?
关于三维余弦定理的证明问题我们可以类比平面中的三角形射影定理来证明三角形余弦定理的方法,给出较简捷的证法.?
先看由三角形射影定理证明其余弦定理的方法:在△ABC中,a、b、c分别表示角A、B、C的对边,则有a=bcosC+ccosB, ①?
b=ccosA+acosC, ②?
c=acosB+bcosA, ③?
①×a-②×b-③×c可得?
a2-b2-c2=-2bccosA,?
∴a2=b2+c2-2bcosA.?
下面给出三维余弦定理的证明,如例4图形,记号![]() 表示面积为S1和S2的两个面所成的二面角大小,由例4的三维射影定理可知:?
表示面积为S1和S2的两个面所成的二面角大小,由例4的三维射影定理可知:?
S=S1cos![]() +S2cos
+S2cos![]() +S3cos
+S3cos![]() ,①?
,①?
S1=S2cos![]() +S3cos
+S3cos![]() +Scos
+Scos![]() ,②?
,②?
S2=S3cos![]() +Scos
+Scos![]() +S1cos
+S1cos![]() ,③?
,③?
S3=Scos![]() +S1cos
+S1cos![]() +S2cos
+S2cos![]() ,④?
,④?
①×S-②×S1-③×S2-④×S3可得?
S2-S12-S22-S32=-2S1S2cos![]() -2S2S3cos
-2S2S3cos![]() -2S3S1cos
-2S3S1cos![]() S3S1?=-2S1S2cosα-2S2S3cosβ-2S3S1cosγ.?
S3S1?=-2S1S2cosα-2S2S3cosβ-2S3S1cosγ.?
移项得欲证三维余弦定理.?
温馨提示:在我们学习空间图形时,常常以四面体和长方体分别作为三角形和矩形的类比物,将二维空间(平面)中的某些常见的定理类比推理到三维空间得出相应的命题.

 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案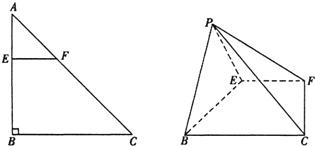
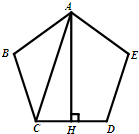 如图,正五边形ABCDE的边长为2,甲同学在△ABC中用余弦定理解得
如图,正五边形ABCDE的边长为2,甲同学在△ABC中用余弦定理解得 如图,正五边形ABCDE的边长为2,甲同学在△ABC中用余弦定理解得
如图,正五边形ABCDE的边长为2,甲同学在△ABC中用余弦定理解得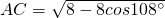 ,乙同学在Rt△ACH中解得
,乙同学在Rt△ACH中解得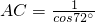 ,据此可得cos72°的值所在区间为
,据此可得cos72°的值所在区间为 ,乙同学在Rt△ACH中解得
,乙同学在Rt△ACH中解得 ,据此可得cos72°的值所在区间为( )
,据此可得cos72°的值所在区间为( )
 ,乙同学在Rt△ACH中解得
,乙同学在Rt△ACH中解得 ,据此可得cos72°的值所在区间为( )
,据此可得cos72°的值所在区间为( )